定義
共軛映射存在定理
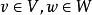 共軛映射
共軛映射設V,W都是Ω上的有限維內積空間。若σ是V到W的一個線性映射,則恰有W到V的一個線性映射σ*與之對應,叫作σ的共軛映射,使對任意 ,有
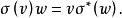 共軛映射
共軛映射證明
 共軛映射
共軛映射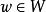 共軛映射
共軛映射設 是V的一個標準正交基底,對任意 ,定義
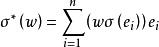 共軛映射
共軛映射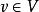 共軛映射
共軛映射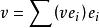 共軛映射
共軛映射易驗證σ*是W到V的一個線性映射,對任意 ,又因 ,於是有
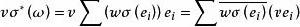 共軛映射
共軛映射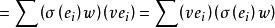 共軛映射
共軛映射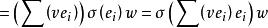 共軛映射
共軛映射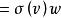 共軛映射
共軛映射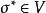 共軛映射
共軛映射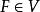 共軛映射
共軛映射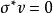 共軛映射
共軛映射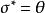 共軛映射
共軛映射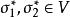 共軛映射
共軛映射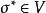 共軛映射
共軛映射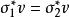 共軛映射
共軛映射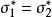 共軛映射
共軛映射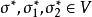 共軛映射
共軛映射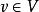 共軛映射
共軛映射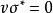 共軛映射
共軛映射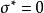 共軛映射
共軛映射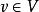 共軛映射
共軛映射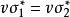 共軛映射
共軛映射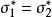 共軛映射
共軛映射設 ,若對任意 都有 ,則 。於是,若 對任意 都有 ,則 對稱地,設 ,若對任意 都有 ,則 ;若對任意 都有 ,則 則由此可說明σ*的唯一性
證明完畢。
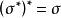 共軛映射
共軛映射顯然有 ,從而可以說σ與σ*互為共軛映射。
共軛轉置矩陣
 共軛映射
共軛映射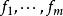 共軛映射
共軛映射設 與 分為Ω上內積空間V與W的標準正交基底,則當
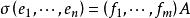 共軛映射
共軛映射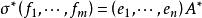 共軛映射
共軛映射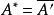 共軛映射
共軛映射時有 其中A*為矩陣A的共軛轉置矩陣,即 。
證明
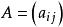 共軛映射
共軛映射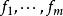 共軛映射
共軛映射 共軛映射
共軛映射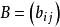 共軛映射
共軛映射記 而σ*在 與 下對應的 ,於是有
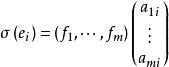 共軛映射
共軛映射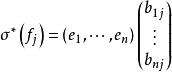 共軛映射
共軛映射從而有
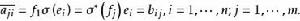 共軛映射
共軛映射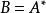 共軛映射
共軛映射於是有 ,證明完畢。
推論
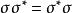 共軛映射
共軛映射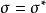 共軛映射
共軛映射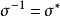 共軛映射
共軛映射1.設σ是Ω上有限維內積空間V的線性變換,如果 ,則說σ是規範的,如果 ,則說σ是自共軛的,而當Ω為實數域時說σ是對稱的,當Ω為複數域時說σ是Hermite的,如果σ可逆且 ,則當Ω為實數域時說σ是正交變換,而當Ω為複數域時說σ是U變換。
 共軛映射
共軛映射系設 是Ω上內積空間y的一個標準正交基底,σ是V的一個線性變換,
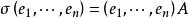 共軛映射
共軛映射,
則:
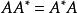 共軛映射
共軛映射(1)σ為規範的充分必要條件是 ,此時稱矩陣A是規範的。
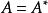 共軛映射
共軛映射(2)σ為對稱(Hermite)的充分必要條件是 ,當Ω為複數域時稱A為Hermite的。
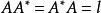 共軛映射
共軛映射(3)σ為正交(U)的充分必要條件是 。
2.設A為一規範矩陣,其第r行元素除對角線元素外都為零,則第r列元素也是這樣。
3.設σ為n維內積空間v的一個線性變換,則下列條件等價:
(1)σ是正交(U)變換;
(2)σ在V的任意標準正交基底下對應正交(U)矩陣;
(3)σ把V的每個標準正交基底都變成標準正交基底;
(4)σ不變向量的長度;
(5)σ不變向量的內積。
共軛映射的個數
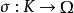 共軛映射
共軛映射設F是一個域,Ω是F的一個代數閉包。K是擴張Ω/F的一個中間域。K到Ω內的一個,F-同態單射叫做K到Ω內的一個F-共軛映射,簡稱為F-共軛。設 是一個F-共軛。那么σ(K)也是Ω/F的一個中間域,並且σ(K)與K是F-共軛的。
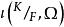 共軛映射
共軛映射令A是K到Ω內的一切F-共軛所成的集。我們把A的基數(K的F-共軛的個數)記作 。
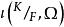 共軛映射
共軛映射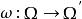 共軛映射
共軛映射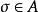 共軛映射
共軛映射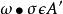 共軛映射
共軛映射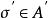 共軛映射
共軛映射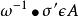 共軛映射
共軛映射不依賴於代數閉包Ω的選取。事實上,設Ω和Ω’都是F的代數閉包並且都包含K。那么存在F-同構映射 。令A和A’分別是K到Ω內的F-共軛和K到Ω’內的F-共軛所成的集。對於任意 ,則 。反過來,對於任意 ,則 。因此,
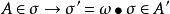 共軛映射
共軛映射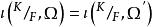 共軛映射
共軛映射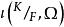 共軛映射
共軛映射是A到A’的雙射,從而 。因此,對於代數擴張K/F來說,我們任意取定F的一個包含K的代數閉包Ω,而把K到Ω內的F-共軛的個數記作 。
