簡介
簡稱旋轉。歐氏幾何中的一種重要變換.即在歐氏平面上(歐氏空間中),讓每一點 P繞一固定點(固定軸線)旋轉一個定角,變成另一點 P′,如此產生的變換稱為平面上(空間中)的旋轉變換。此固定點(固定直線)稱為旋轉中心(旋轉軸),該定角稱為旋轉角。旋轉是第一種正交變換。
發音:旋(xuán)轉(zhuàn )。英文:rotation
在平面內,把一個圖形繞點O旋轉一個角度的圖形變換叫做旋轉,點O叫做旋轉中心,旋轉的角叫做旋轉角,如果圖形上的點P經過旋轉變為點Pˊ,那么這兩個點叫做這個旋轉的對應點。
性質
: ①對應點到旋轉中心的距離相等(意味著:旋轉中心在對應點所連線段的垂直平分線上)。
②對應點與旋轉中心所連線段的夾角等於旋轉角。 ③旋轉前、後的圖形全等。
 旋轉變換
旋轉變換旋轉三要素: ①旋轉中心;
②旋轉方向;
③旋轉角度。
注意:三要素中只要任意改變一個,圖形就會不一樣。
旋轉變換的作圖:①確定旋轉中心、旋轉方向和旋轉角度;②找出能確定圖形的關鍵點;③連結圖形的關鍵點與旋轉中心,並按旋轉的方向分別將它們旋轉一個角,得到此關鍵點的對應點;④按原圖形的順序連結這些對應點,所得圖形就是旋轉後的圖形。
旋轉對稱性:如果某圖形繞著某個定點轉動一定角度(小於360°)後能與自身重合,那么這種圖形就叫做旋轉對稱圖形。 (結合網路及教輔書籍)
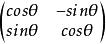 旋轉變換
旋轉變換假設初始點P=(Xo,Yo)T 中心點O(Cx,Cy)T 矩陣A[2×2]=
(T表示轉置,θ為從P到P'的旋轉角差值)
那么P'=A×(P-O)+O
即 P'=((Xo-Cx)×cosθ-(Yo-Cy)×sinθ+Cx,(Xo-Cx)×sinθ+(Yo-Cy)×cosθ+Cy)
證明:
設圓心為O(Cx,Cy)T ,半徑為r=|P-O|的圓C為:
x=Cx+r×cosα
y=Cy+r×sinα
則P點位於圓上,設向量(OP)與x軸夾角是β;
另設一點P'在圓上,且向量(OP)與向量(OP')的夾角是θ,可得:
P'x=Cx+r×cos(β+θ)=Cx+(r×cosβ)×cosθ-(r×sinβ)×sinθ -----------①
P'y=Cy+r×sin(β+θ)=Cx+(r×sinβ)×cosθ+(r×cosβ)×sinθ -----------②
由於:
Xo=Cx+r×cosβ
Yo=Cy+r×sinβ
得到:
r×cosβ=Xo-Cx
r×sinβ=Yo-Cy
代入①②得:
P'x=Cx+(Xo-Cx)×cosθ-(Yo-Cy)×sinθ
P'y=Cy+(Yo-Cy)×cosθ+(Xo-Cx)×sinθ
即:
P'=((Xo-Cx)×cosθ-(Yo-Cy)×sinθ+Cx,(Xo-Cx)×sinθ+(Yo-Cy)×cosθ+Cy)
寫作矩陣形式:
P'=A×(P-O)+O
其中:
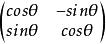 旋轉變換
旋轉變換P=(Xo,Yo)T O(Cx,Cy)T 矩陣A[2×2]=