簡介
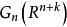 施蒂費爾流形
施蒂費爾流形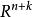 施蒂費爾流形
施蒂費爾流形格拉斯曼流形 是通過坐標空間 的原點的所有 n 維平面的集合,這可以視為一個商空間。
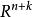 施蒂費爾流形
施蒂費爾流形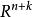 施蒂費爾流形
施蒂費爾流形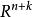 施蒂費爾流形
施蒂費爾流形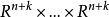 施蒂費爾流形
施蒂費爾流形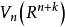 施蒂費爾流形
施蒂費爾流形的一個 n 標架是 中線性無關向量的一個 n 元組, 中的所有 n 標架的全體構成 n重直積 的一個開子集,稱其為施蒂費爾流形 。
性質
格拉斯曼流形有一個標準映射
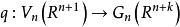 施蒂費爾流形
施蒂費爾流形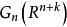 施蒂費爾流形
施蒂費爾流形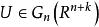 施蒂費爾流形
施蒂費爾流形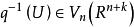 施蒂費爾流形
施蒂費爾流形它把每個n標架映為它所生成的n平面,給 以商拓撲如下:子集 是開集的充分必要條件是 q 的逆映射的像 是開集。
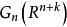 施蒂費爾流形
施蒂費爾流形格拉斯曼流形 是nk維緊光滑流形。
商空間
(quotient space)
線上性代數中,一個向量空間V被一個子空間N的商是將N“坍塌”為零得到的向量空間,所得的空間稱為商空間,記作V/N(讀作V模N)。
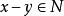 施蒂費爾流形
施蒂費爾流形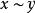 施蒂費爾流形
施蒂費爾流形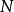 施蒂費爾流形
施蒂費爾流形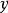 施蒂費爾流形
施蒂費爾流形 施蒂費爾流形
施蒂費爾流形設V是域K上的一個向量空間,且N是V的一個子空間。我們定義在V上定義一個等價類,如果 則令 。即如果其中一個加上 中一個元素得到另一個,則與 相關。 的所在等價類通常記作
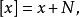 施蒂費爾流形
施蒂費爾流形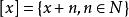 施蒂費爾流形
施蒂費爾流形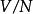 施蒂費爾流形
施蒂費爾流形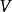 施蒂費爾流形
施蒂費爾流形 施蒂費爾流形
施蒂費爾流形 施蒂費爾流形
施蒂費爾流形因為它由 給出。那么商空間 定義為 / ,V在 下所有等價類集合。
