測試方法
壓痕法(IM)
測試試樣表面先拋光成鏡面,在顯微硬度儀上,以10Kg負載在拋光表面用硬度計的錐形金剛石壓頭產生一壓痕,這樣在壓痕的四個頂點就產生了預製裂紋。根據壓痕載荷P和壓痕裂紋擴展長度C計算出斷裂韌性數值(KIC)。 計算公式為:
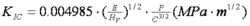 計算公式
計算公式E為楊氏模量,例如對於Si3N4系統一般取300GPa。公式中載荷P單位為N, 裂紋長度C單位為mm, 顯微硬度HV單位為GPa。
 壓痕法實例圖
壓痕法實例圖試樣類型
目前國內常用的斷裂韌性試樣有兩種:
1)三點彎曲試樣SE(B)
2)緊湊拉伸試樣C(T)
試驗方法
在試樣中間開一裂紋,通過三點或四點抗彎斷裂測試,計算材料的斷裂韌性。
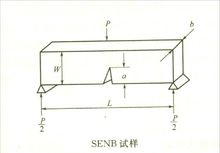 SENB
SENB測試方法比較
·IM法比SENB法簡便經濟,但測得的數據不如SENB法可靠;
·SENB法是普遍公認的標準測試方法;
·為了實際方便,要對IM法測試公式修正,使結果更接近SENB法。
研究進展
隨著機率斷裂力學工程套用的逐步深入,材料斷裂韌性分散性問題,已成為影響含缺陷結構機率安全評定的關鍵因素之一。合理解決材料斷裂韌性分散性是一個十分複雜的問題。一方面由於冶金過程等方面的偏差,造成材料斷裂韌性的分散性;另一方面由於試樣幾何尺寸、裂紋 長度測量等 試驗誤差,亦會導致測試結果的不確定性,還有不同測試規範和標準對測試數據的處理也會導致測試結果的不確定性。若缺陷位於焊接部位,影響因素將更加複雜。除上述原因外,還會有諸如焊接上藝、焊材、以及不同操作人員及焊後熱處理等因素導致斷裂韌性測試結果分散性更加嚴重。儘管分析和解決其分散性問題如此複雜,十分困難,然而,在對含缺陷焊接結構(尤其是工業鍋爐、壓力容器和管道)進行安全評定時,重點就是焊接接頭區而不是母材。如何處理斷裂韌性的分散性問題已成為工程界不可迴避的問題,也是機率安全評定應解決的基本問題之—。
對材料斷裂韌性 分散性規律的研究,在理論和實踐上均已取得較大進展。
Wallin分別根據Weibuli 統計模型和 微結構 分析模型,推得基於斷裂韌性尺I(單位:MN·m-3/2)失效準則的累積失效機率
並從理論上得到Kl服從形狀參數m:為4的Weibull分布,同時指出m1不等於4是由於測試數據不夠而造成的,並且認為延性撕裂和材料非均勻性對 分散性只具有較輕微的影響。這一理論建立在裂尖小範圍有效體積基礎上。
Slatcher將裂尖等效為多個單元的串聯模型,推導出基寸: 斷裂韌性,J(單位:N/inlTl)失效準則的累積失效機率
式中,a=B中,B為試樣寬度,中為常數;B=2。
這一理淪基於如下假設:
1)裂紋體能被分成若干單元,任一單元的失效意味著整體失效,各單元強度彼此獨立且同分布。
2)第一個失效單元的應力和應變與裂尖應力場強度,J和該單元到裂尖的垂直距離r有關,僅由r/J確定。
3)第一個失效單元必須位於r和O定義的區域內(r,O為該單元的柱坐標)對任何O均有Jg(O)≤r≤Jh(O)。g(O)和h(O))為o的函式,分別為該區域的內、外界限。
由式(5.2)可知,理論上斷裂韌性/服從形狀參數為2的雙參數威布爾分布。對充分小的試驗數據集,式(5.2)比 對數常態分配和 威布爾分布能更好地描述斷裂韌性的分布規律。
Neville提出了另一種描述斷裂韌性分布的模型,該模型不用作任何假設和近似處理。由斷裂韌性構成一個樣本u,樣本u中的子樣ui由g2,J2或K1確定,g2,J2或K1分別由CTOD、JIC和Kic的測試數據計算得到。累積失效機率由如下雙參數 分布函式表達
式中,a,b為分布參數。
Neville將該模型分別對幾組斷裂韌性的測試數據進行了分析,結果表明該模型套用方便,與實測數據分布吻合較好,並略偏保守。
Hauge和Thualow分別採用Weibull分布、Log—Normal分布、Slather模型以及Neville模型,對兩組CTOD數據(86個母材和16個焊材)進行了統計分析,其主要結論如下:
1)兩組CTOD數據並非服從形狀參數為2的Weibull分布(或Slather模型);雙參數Weibull分布、Log—Normal分布和Neville分布都適宜 擬合這些數據。
2)90%置信限的中位期望值可較好地由I.og—Normal分布得到;對於只有三個子樣時,能較好地等效於三個值十取最小值的方法;對大子樣,Log—Normal吻合更好。
3)對於小子樣,Log—Normal分布提供最為可靠的估計,Weibull分布和Neville模型在於樣為3和5時由於數據不夠,難以估計分布參數值。
4)數值模擬結果及 擬合結果均表明Log—Normal分布無論對太子樣還是小於樣,擬合精度足夠,不是特別保守。
Mimura等對由於材料不均勻而引起斷裂韌性的分散性做了分析與試驗研究。經過從同一塊板上取樣的CharpyV型試塊試驗分析,提出了區別材料不均勻性導致的分散性與測試中導致的分散性的方法。
論文
聚烯烴彈性體POE作為一種新型彈性體,具有良好的加工性能和力學性能,相比EPDM與EPR等彈性體而言對聚丙烯的增韌效果更好。但目前尚未有文獻研究POE對PP斷裂韌性的影響,本文採用了一種新近發展起來的研究斷裂韌性的方法-基本斷裂功法(EWF),研究了PP和不同含量POE的PP/POE共混體系的斷裂韌性,同時分析了其力學性能。
本文採用注射成型的雙邊深缺口拉伸(DENT)試樣在 室溫及低速應力(5mm/min)條件下進行拉伸斷裂實驗。根據EWF理論[2,],拉斷帶缺口試樣所需的總斷裂功Wf可分為兩部分:基本斷裂功We和非基本斷裂功或塑性功Wp。We用於形成新的斷裂表面,為 表面能,對一定厚度(t)的試樣,它與試樣韌帶(ligament)即缺口剩餘長度(l)成正比,Wp是消耗於 塑性變形的那部分功,為體積能,與l2成正比。
