斜面[簡單機械]

斜面所屬現代詞，指的是同水平面成一傾斜角度的平面，這個角度通常稱為升角。

基本信息

• 中文名：斜面
• 其他外文名：inclined plane，bevel face，oblique plane

• 解釋：與水平方向有不為零的夾角平面
• 分類：凸形斜面，凹形斜面
• 用途：克服垂直提升重物之困難等

概念解析

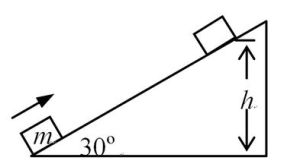斜面

斜面是一種簡單機械，可用於克服垂直提升重物之困難，省力但是費距離。距離比和力比都取決於傾角：斜面與平面的傾角越小，斜面較長，則省力越大，但費距離。斜面與平面的傾角越大，斜面較短，則省力越小，但省距離。斜面在生活中有廣泛的套用，如盤山公路、搬運滾筒、斜面傳送帶等。在不計算任何阻力時，斜面的機械效率為100%，如果摩擦力很小，則可達到很高的效率。即用F2表示力，s表示斜面長，h表示斜面高，物重為G。不計無用阻力時，根據功的原理，可得：F2s=Gh

受力情況

物體靜止在斜面上受到這些力：物體自身的重力（G），斜面對之的支持力（F支），對物體的摩擦力（f靜）等。已知斜面的傾角和物體的重力時，我們可以求出另外的兩個力：
設斜面傾角為θ，其他和上述一樣，則我們把重力分解成沿著斜面的垂線向下的
力F1（F1=F支）和平行於斜面向下的力F2。（當物體靜止在斜面上時，F2=f。注意到這裡的施力物體是地球，不是斜面上的物體），建立平行四邊形後，我們可以看到重力邊和F2的夾角為90-θ。

分類

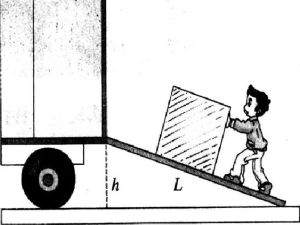斜面

從山頂到山腳的傾斜面叫斜面，也叫斜坡或山坡。在地圖上明確斜面的具體形狀，對定向越野有一定價值。斜面按其形狀可分為：實地坡度基本一致的斜面叫等齊斜面，全部斜面均可通視。地圖上，從山頂到山腳，間隔基本相等的一組等高線，表示為等齊斜面。

凸形斜面

實地坡度為上緩下陡的斜面叫凸形斜面，部分地段不能通視。地圖上，從山頂到山腳，間隔為上面稀、下面密的一組等高線，表示為凸形斜面。

凹形斜面

實地坡度為上陡下緩的斜面叫凹形斜面，全部斜面均可通視。地圖上，從山頂到山腳，間隔為上面密、下面稀的一組等高線，表示為凹形斜面。

波狀斜面

實地坡度交叉變換、陡緩不一、成波狀形的不規則斜面叫波狀斜面，若干地段不能通視。地圖上，表示該狀斜面的等高線間隔稀密不均，沒有規律。

套用

日常生活中所用的螺絲釘，就是斜面原理的最好體現。其他的還有金字塔、樓梯、登機橋、電梯、盤山公路等。

機械效率公式

對於一般斜面來說，如果不計算任何的阻力，根據功的原理，斜面的機械效率是100%，但是不可避免存在一些阻力，如摩擦力和空氣阻力。下面我們就著摩擦力來計算機械效率。我們用θ表示斜面的傾角，G表示物重，Fl表示拉力，fm表示摩擦力，μ表示斜面摩擦力係數，s表示斜面長，h表示斜面高，Wy表示有用功，Wz表示總功，We表示額外功，而F2是順著斜面向下的分力，這些都在“受力情況”一節有提到。