文獻分布定律
正文
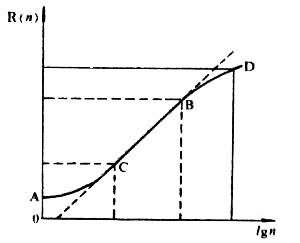
定量描述某一學科論文在相關期刊中的分布規律。該定律指出:如果將科學期刊按某一給定學科的論文刊載量多少,以遞減順序排列起來,就可以將這些期刊分成專門論述該學科的“核心”區和另外幾個組或區,其中每區期刊的載文量與核心區期刊載文量相等,這時各區的期刊數成1:n:n2…。n為布拉德福常數,n>1。該定律於1934年1月26日 在《工程》周刊上由英國文獻學家S.C.布拉德福首先提出,故又稱為布拉德福定律、布拉德福分布定律或布氏定律。布拉德福定律還可以用圖像表示。如果取等級排列的期刊序號(級數)的對數(lgn) 為橫坐標,以相應的論文累積數【R (n)】為縱坐標繪製成圖,便得到一條曲線,稱為布拉德福分布曲線,如圖所示。
 文獻分布定律
文獻分布定律文獻分布定律雖然在1934年就已提出,但並未引起學術界重視。直到1948年布拉德福在他的專著《文獻工作》中對該定律作進一步論述之後,才引起人們關注。其中最有代表性的當推英國的B.C.維克里和B.C.布魯克斯。維克里推廣和修正了布拉德福定律,使布拉德福文獻分布的圖像與定律在結構上得到了統一,形式上趨於完整。布魯克斯則以數學公式較為嚴密地描述了這一定律,發展了圖像分析方法,為其實際套用開拓了新路。正是由於許多學者的共同努力,才使布拉德福定律從理論上和套用上日趨完善並迅速發展起來。
布拉德福定律不僅對情報學的理論研究有重要影響,而且實際套用相當廣泛,如對於確定核心期刊,制定文獻採購策略,藏書政策,最佳化館藏,檢驗文獻服務工作情況,掌握讀者閱讀傾向,檢索利用文獻等方面都有一定指導作用。
布拉德福定律同時也具有一定局限性。它必須充分滿足下列條件才能成立:①論文所屬的學科或專業領域應當清楚劃定;②被分析的某一學科、領域或主題的期刊清單,以及對這些期刊中所刊載的相關論文的統計應當是充分的;③被分析的期刊的時間應當清楚限定,以便使這些期刊上刊載的相關論文都被計算出來。其套用也常受這些條件限制。
科學論文的分布是一個很複雜的問題,既受人的主觀因素影響,又受客觀條件限制。布拉德福定律已經從數量上初步揭示了這一分布規律。今後要綜合運用多種數學工具,以大量的統計數據為基礎,同時考慮多種影響因素,建立更為普遍適用的數學模型和檢驗手段,使布拉德福定律更加完善,並有效地付諸實用。
