數據處理的分組方法

數據處理的分組方法

正文

對結構未知的複雜非線性系統的一種啟發式自組織建模方法，簡稱GMDH法。這種方法是用輸入變數的多項式來近似地表示非線性系統的輸入輸出關係。一般的非線性輸入輸出關係可表示為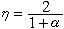

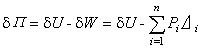式中y是輸出變數；是輸入變數;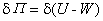的多項式。直接計算十分困難,甚至是不可能的。60年代末期,蘇聯生物控制論學者И,赫寧柯借鑑生物控制論中的自組織化的方法提出GMDH法。它的思路不同於其他任何最佳化算法。這個算法是多層型的，每一層用輸入輸出數據擬合得到輸入變數兩兩組合而成的部分表示。它是兩個變數的函式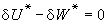，一般可取G為二次完全多項式：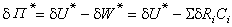　

然後將所得到的部分表示，用誤差平方和按一定的閾值淘汰一部分，將留下的部分表示作為下一層的輸入變數，再按同樣的辦法得到新的一層的部分表示。在新的一層再對部分表示進行篩選，保留一部分作為下一層的輸入。這樣一層一層地選下去直到選出符合要求的部分表示。將最後選到的部分表示回代成原始的輸入變數，即得到最終的模型，這就是多層型信息處理的建模方法。
GMDH算法可歸結為以下的基本步驟：①對原始的輸入變數進行預備性選擇。②為了決定部分表示的係數和對每一層的中間變數的正確的選擇，將數據分成擬合組（用於決定係數）和檢驗組（用於選擇部分表示），並給出數據分組的原則和方法。③產生兩個變數為基礎的部分表示。④按多層結構給出各層的閾值，使得算法過程中能自動選擇部分表示。⑤選出最終模型。
GMDH算法對於難以從先驗知識得到模型結構的複雜的非線性系統的建模是很有效的。特別是在輸入變數多而數據很少的情況下，其他建模方法很少能奏效，GMDH算法的優越性就更為明顯。它在許多方面，例如在巨觀經濟模型、人口模型、大氣污染模型、水質模型、各種預報模型、工業過程控制模型等方面都得到了成功的套用。
參考書目
　夏天長著，熊光楞、李芳芸譯：《系統辨識》，清華大學出版社，北京,1983。(T.C.Hsia,Identification: Least-Squeres Methods，Lexington books, Lexington， Mass.,1977.)

配圖

相關連線