基本介紹
數值方程是量的數值間的關係式。由於量的數值與量所採用的單位有關，所以數值方程的形式與其中量所採用的單位有關。而且，在給出數值方程時，必須指明其中各個量所採用的單位。
關於數值的詳細說明見下文小節。
舉例說明
數值方程
數值方程
數值方程在速度 ；長度 和時間 之間的量方程為：
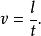數值方程當採用km/h；m和s分別作為速度；長度和時間的單位時，導出的數值方程為：
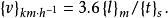數值方程這個式子的含義是：當長度以m作為單位的數值除以時間以s作為單位的數值所得之商，必須乘以3.6後才是以km/h作為單位的速度數值。
上述數值方程可寫成：
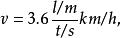數值方程但不可寫成：
數值方程也不應寫成：
數值方程因為上述第一種寫法，雖有花括弧說明是數值，但卻未指明單位；上述第二種寫法，這些量的符號是量？還是數？是不明確的。
但是，在工程技術界，大量地存在上述的第二種寫法。
例如：
以鹽酸標準滴定溶液作滴定劑測定某一物質的鹼度，該鹽酸標準滴定溶液確定了的濃度為c(HCI)=0.2 mol/L。其結果以氫氧化鉀(KOH)的質量分數表示，其計算方法為：
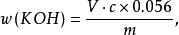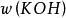數值方程
數值方程式中：為KOH的質量分數，以%為單位；
數值方程為所消耗鹽酸標準滴定溶液的體積，mL；
c(HCl)為鹽酸標準滴定溶液的濃度，mol/L；
m為試料的質量，g；
0.056為氫氧化鉀的摩爾質量，即M(KOH)，它等於0.056，以kg/mol為單位。
上述式子所用符號均為量的符號，但卻只代表其量值中特定單位（在符號說明中指出）的數值，實際上是個數值方程。這個數值方程中所選用的單位，由於考慮到了等號左右單位的相等，在其形式上卻完全與量方程一致。
等號左邊的單位為：1；
等號右邊的單位為：
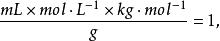數值方程因而未引入新的係數。
數值的表達形式
由於量A的量值表達為：
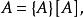數值方程其中：[A]為量A所採用的單位；而{A}則為採用[A]作為單位時A所具有的數值。因此，數值：
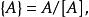數值方程這是 數值的第一種表達式。
例如：
v/km·h：以公里每小時作為單位表達速度的數值；
c(H )/mmol·L ：以毫摩爾每升作為單位表達H 在溶液中的濃度的數值。
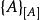數值方程數值的第二種表達形式為：。
即以所採用的單位作為花括弧的下標給出。這裡，花括弧已表達為一個數值，但必須交待的單位則作為下標。這種形式，同樣是確切的。
例如：
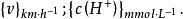數值方程由於第二種形式採用了下角標，在印刷上比較複雜，實際使用較少。
上述數值的表達形式的使用主要有以下三種場合：
a) 表格中的表頭；
b) 坐標；
c) 數值方程。
關於數值的表達，不宜使用諸如：
a) 米數；
b) 摩爾數；
c) 安培數之類的形式。
因為上述三例中，米和摩爾固然只是用於表示長度和物質的量的單位而不致導致混淆，但安培數則既可用於表示電流，也可用於表示磁通勢(按SI的規定，磁通勢的SI單位也是安培)。
更不應將它們作為量的概念，例如：把物質的量稱為摩爾數；把長度稱為米數。
