積分方程數值解的主要求解對象為第一、二類弗雷德霍姆型和伏爾泰拉型積分方程以及相應的特徵值問題.主要求解方法有伽遼金法，配置法和求積法.下面以第二類弗雷德霍姆型積分方程
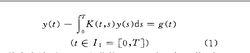積分方程數值解法(其中右端項g (t)，積分核KCt,s)為已知函式)為例，介紹上述三種數值方法:
1.伽遼金法.將區間1=[0,T」剖分成若干個小區間。=to<t, <... <tn=T，在此剖分基礎上建立分片多項式空間
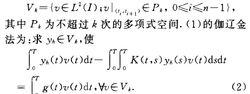積分方程數值解法2.配置法.如前所述建立r一 [o,T」的剖分及分片多項式空間vk，在每個小區間[t; , t;+l〕上，取k+1個配置點{z、，、}k+z=.> ;;二〔t,,t;+n (}=0,1,...}，一1).方程(1)的配置法為:求yhEv*使
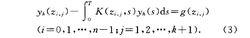積分方程數值解法3.求積法.同上將1=Co>T」分成n個小區間，將方程(1)中的積分項在每個小區間上作數值積分，得到
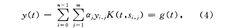積分方程數值解法其中、，，為區間巨，，乙十i」上的積分點，a、為相應的數值積分系·令(4)式中t=s;,; (i一。}1,...}n-1}}=1,2,"..,m)，則得到一組以y. ; _-__ y (S.， ;)為未知量的線性代數方程組.求解此方程組即可得到求積法之近似解在點s; ,;的值y%，.
若配置法中的配置點{z、，，}取數值積分的積分點，且(3)式中的積分項用相應的數值積分代替，則此法與求積法等價.
除上述三種常見的積分方程數值解法外，還有一些其他有效算法，如疊代的伽遼金法及配置法，伏爾泰拉線性多步法或龍格一庫塔法，求解奇異積分方 程的特殊方法等.
