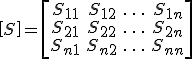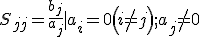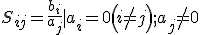散射矩陣

散射矩陣是物理學中描述散射過程的一個主要觀測量。

散射矩陣,又稱S矩陣,是物理學中描述散射過程的一個主要觀測量。
現代高能物理的發展，同其他物理學一樣是理論和實驗的互動，而這種互動主要的橋樑就是散射矩陣。
假設散射源為很好的定域散射源，與被散射粒子的相互作用局限在有限的空間範圍內，那么，無窮遠時間以前粒子處於一個自由態，稱為入態，記為|Ψ>in；無窮遠時間之後粒子也是處於一個自由態，稱為出態，記為|Ψ>out。 入態到初態，相互作用可以用一個矩陣描述，記為S，那么就有：
|Ψ>out=S |Ψ>in
這就是散射矩陣的定義。
散射矩陣直接與可觀測的物理量相聯繫，但是我們在量子場論中處理的是場，兩者如何聯繫？或者說如何從量子場論計算散射矩陣？我們還要利用一個LSZ約化規則，它聯繫了量子場論中的格林函式和可觀測的散射矩陣。這使得理論能夠預言實驗。
散射矩陣（scattering matrix） 在微波元件中表示網路特性的參量之一，在n連線埠線性網路中，描述各連線埠歸一化入射電壓波a與歸一化反射電壓波b之間的關係為[b]=[S][a]，其中

稱為散射矩陣，各矩陣元素Sij稱為散射參量，其優點是在微波網絡中便於測量，且有

Sjj和Sij分別表示除第j連線埠接信號源外其餘連線埠全部接匹配負載時，第j連線埠的歸一化電壓反射係數和從第j連線埠到第i連線埠的歸一化電壓傳輸係數。