放射性衰變規律
正文
指放射性核素的原子數或活度隨時間而改變的規律(見放射性、核素)。1903年E.盧瑟福和F.索迪提出的放射性衰變理論首先揭示了放射性物質的不穩定性,並且在研究釷 X(224Ra)的放射性衰變率時提出了定量的負指數關係式。它的現代表示方式是: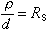 (1)
(1)
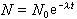 (2)
(2)
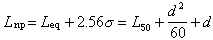 (3)
(3)
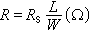 是放射性核素原子的衰變率;NO和N是起始時刻(t=0)和t時刻該核素原子的數目;AO和A是起始時刻和t時刻的活度;λ 是衰變常數,其物理意義是單位時間內原子核的衰變幾率。
是放射性核素原子的衰變率;NO和N是起始時刻(t=0)和t時刻該核素原子的數目;AO和A是起始時刻和t時刻的活度;λ 是衰變常數,其物理意義是單位時間內原子核的衰變幾率。 式(2)表示原子核衰變的統計規律,即放射性原子核的數目隨時間按指數規律減少。每一种放射性核素單獨衰變時都服從這一基本規律,但是各自具有特徵的衰變常數。如鈾238的 λ為1.55×10-10年-1,鐳226的λ為4.33×10-4年-1。原子核的衰變有時是一代又一代地連續進行,這些混在一起的衰變情況非常複雜。
兩次連續衰變規律 母體(核素1)衰變成子體(核素2),子體衰變成穩定核素,且母子體處於同一體系中。這時式(1)和式(2)可以計算不同時間核素 1和孤立的核素2的原子數。與核素1共同存在的核素 2的改變速率應該包括兩部分,一部分是核素1的衰變而產生核素2,另一部分是核素2的衰變。所以:
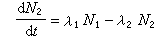 (4)
(4)
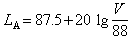 (5)
(5)
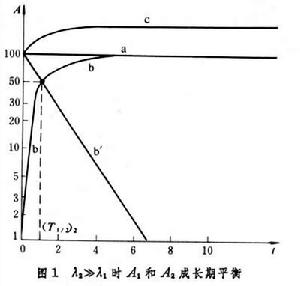
①λ2》λ1 核素2的活度(A2)最初隨時間而增加,然後達到某一飽和值,與核素1的活度(A1)相等,隨後核素2的活度一直按核素1的半衰期衰減,出現長期平衡(圖1)。曲線 c是核素1和2的活度總和,曲線a是開始時純粹核素1的活度,曲線 b是從純粹核素 1中逐漸積累的核素 2的活度,曲線b′是孤立的核素2的活度隨時間衰減的狀況。鈾238中產生釷234,鐳226中產生氡222都屬於這種情況。另外,利用反應堆中的中子或加速器產生的離子束通過核反應生產放射性核素時,只要核反應速率保持恆定,放射性核素的活度變化也與長期平衡狀況一致。
 放射性衰變規律
放射性衰變規律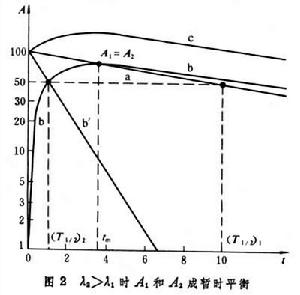 放射性衰變規律
放射性衰變規律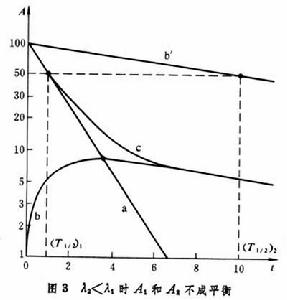 放射性衰變規律
放射性衰變規律多次連續衰變規律 1910年英國數學家H.貝特曼得到了這一過程的解。原則上不論有多少成員的放射性衰變系列,數學求算各代成員的原子數和活度都是可能的。實際上中間成員常常可以忽略,一般以考慮兩代放射性核素(即母子體)的情況為最普遍。
根據放射性衰變規律,除了計算放射性核素的原子數和活度(這方面的用途很多,如用於放射性核素的生產和地質樣品年齡的測算中)以外,通過曲線分析還可以求出放射性核素的半衰期。