簡介
 支持向量機
支持向量機支持向量機方法是建立在統計學習理論的VC維理論和結構風險最小原理基礎上的,根據有限的樣本信息在模型的複雜性(即對特定訓練樣本的學習精度)和學習能力(即無錯誤地識別任意樣本的能力)之間尋求最佳折衷,以期獲得最好的推廣能力。
總體概述
在機器學習中,支持向量機(SVM,還支持矢量網路)是與相關的學習算法有關的監督學習模型,可以分析數據,識別模式,用於分類和回歸分析。給定一組訓練樣本,每個標記為屬於兩類,一個SVM訓練算法建立了一個模型,分配新的實例為一類或其他類,使其成為非機率二元線性分類。一個SVM模型的例子,如在空間中的點,映射,使得所述不同的類別的例子是由一個明顯的差距是儘可能寬劃分的表示。新的實施例則映射到相同的空間中,並預測基於它們落在所述間隙側上屬於一個類別。
除了進行線性分類,支持向量機可以使用所謂的核技巧,它們的輸入隱含映射成高維特徵空間中有效地進行非線性分類。
詳細介紹
更正式地說,一個支持向量機的構造一個超平面,或在高或無限維空間,其可以用於分類,回歸,或其它任務中設定的超平面的。直觀地,一個良好的分離通過具有到任何類(所謂官能餘量)的最接近的訓練數據點的最大距離的超平面的一般實現中,由於較大的裕度下分類器的泛化誤差。
而原來的問題可能在一個有限維空間中所述,經常發生以鑑別集是不是在該空間線性可分。出於這個原因,有人建議,在原始有限維空間映射到一個高得多的立體空間,推測使分離在空間比較容易。保持計算負荷合理,使用支持向量機計畫的映射被設計成確保在點積可在原空間中的變數而言容易地計算,通過定義它們中選擇的核函式k(x,y)的計算以適應的問題。
在高維空間中的超平面被定義為一組點的點積與該空間中的向量是恆定的。限定的超平面的載體可被選擇為線性組合與參數\alpha_i中發生的數據的基礎上的特徵向量的圖像。這種選擇一個超平面,該點中的x的特徵空間映射到超平面是由關係定義:\字型\sum_i\alpha_ik(x_i中,x)=\mathrm{常數}。注意,如果k(x,y)變小為y的增長進一步遠離的x,在求和的每一項測量測試點x的接近程度的相應數據基點x_i的程度。以這種方式,核心上面的總和可以被用於測量各個測試點的對數據點始發於一個或另一個集合中的要被鑑別的相對接近程度。注意一個事實,即設定點的x映射到任何超平面可以相當卷積的結果,使集未在原始空間凸出於各之間複雜得多歧視。
動機
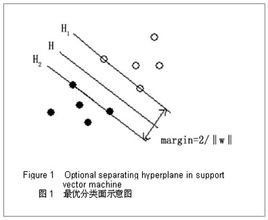
我們通常希望分類的過程是一個機器學習的過程。這些數據點是n維實空間中的點。我們希望能夠把這些點通過一個n-1維的超平面分開。通常這個被稱為線性分類器。有很多分類器都符合這個要求。但是我們還希望找到分類最佳的平面,即使得屬於兩個不同類的數據點間隔最大的那個面,該面亦稱為最大間隔超平面。如果我們能夠找到這個面,那么這個分類器就稱為最大間隔分類器。
支持向量
所謂支持向量是指那些在間隔區邊緣的訓練樣本點。 這裡的“機(machine,機器)”實際上是一個算法。在機器學習領域,常把一些算法看做是一個機器。
支持向量機(Support vector machines,SVM)與神經網路類似,都是學習型的機制,但與神經網路不同的是SVM使用的是數學方法和最佳化技術。
支持原因
支持向量機將向量映射到一個更高維的空間裡,在這個空間裡建立有一個最大間隔超平面。在分開數據的超平面的兩邊建有兩個互相平行的超平面。建立方向合適的分隔超平面使兩個與之平行的超平面間的距離最大化。其假定為,平行超平面間的距離或差距越大,分類器的總誤差越小。
一個極好的指南是C.J.CBurges的《模式識別支持向量機指南》。
技術支持
支持向量機是由Vapnik領導的AT&T Bell實驗室研究小組在1995年提出的一種新的非常有潛力的分類技術,SVM是一種基於統計學習理論的模式識別方法,主要套用於模式識別領域。由於當時這些研究尚不十分完善,在解決模式識別問題中往往趨於保守,且數學上比較艱澀,這些研究一直沒有得到充分的重視。
直到90年代,統計學習理論 (Statistical Learning Theory,SLT)的實現和由於神經網路等較新興的機器學習方法的研究遇到一些重要的困難,比如如何確定網路結構的問題、過學習與欠學習問題、局部極小點問題等,使得SVM迅速發展和完善,在解決小樣本、非線性及高維模式識別問題中表現出許多特有的優勢,並能夠推廣套用到函式擬合等其他機器學習問題中。從此迅速的發展起來,已經在許多領域(生物信息學,文本和手寫識別等)都取得了成功的套用。
在地球物理反演當中解決非線性反演也有顯著成效,例如(支持向量機在預測地下水湧水量問題等)。已知該算法被套用的主要有:石油測井中利用測井資料預測地層孔隙度及粘粒含量、天氣預報工作等。
支持向量機中的一大亮點是在傳統的最最佳化問題中提出了對偶理論,主要有最大最小對偶及拉格朗日對偶。
SVM的關鍵在於核函式。低維空間向量集通常難於劃分,解決的方法是將它們映射到高維空間。但這個辦法帶來的困難就是計算複雜度的增加,而核函式正好巧妙地解決了這個問題。也就是說,只要選用適當的核函式,就可以得到高維空間的分類函式。在SVM理論中,採用不同的核函式將導致不同的SVM算法。
在確定了核函式之後,由於確定核函式的已知數據也存在一定的誤差,考慮到推廣性問題,因此引入了鬆弛係數以及懲罰係數兩個參變數來加以校正。在確定了核函式基礎上,再經過大量對比實驗等將這兩個係數取定,該項研究就基本完成,適合相關學科或業務內套用,且有一定能力的推廣性。當然誤差是絕對的,不同學科、不同專業的要求不一。
支持向量機的理解需要數據挖掘或機器學習的相關背景知識,在沒有背景知識的情況下,可以先將支持向量機看作簡單分類工具,再進一步引入核函式進行理解。