耦合性
耦合性(英語:Coupling,dependency,或稱 耦合力或 耦合度)是一種軟體度量,是指一程式中,模組及模組之間信息或參數依賴的程度。
內聚性是一個和耦合性相對的概念,一般而言低耦合性代表高內聚性,反之亦然。耦合性和內聚性都是由提出結構化設計概念的賴瑞·康斯坦丁所提出。低耦合性是結構良好程式的特性,低耦合性程式的可讀性及可維護性會比較好。
耦合性的分類
概述
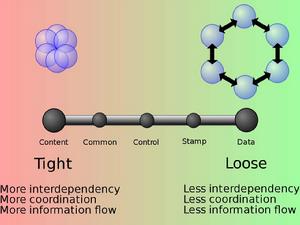
耦合性可以是低耦合性(或稱為鬆散耦合),也可以是高耦合性(或稱為緊密耦合)。以下列出一些耦合性的分類,從高到低依序排列:
內容耦合(content coupling,耦合度最高):也稱為病態耦合(pathological coupling)當一個模組直接使用另一個模組的內部數據,或通過非正常入口而轉入另一個模組內部。
共用耦合/公共耦合(common coupling):也稱為全局耦合(global coupling.)指通過一個公共數據環境相互作用的那些模組間的耦合。公共耦合的複雜程式隨耦合模組的個數增加而增加。
外部耦合(external coupling):發生在二個模組共用一個外加的數據格式、通信協定或是設備界面,基本上和模組和外部工具及設備的溝通有關。
控制耦合(control coupling):指一個模組調用另一個模組時,傳遞的是控制變數(如開關、標誌等),被調模組通過該控制變數的值有選擇地執行塊內某一功能;
特徵耦合/標記耦合(stamp coupling):也稱為數據結構耦合,是指幾個模組共享一個複雜的數據結構,如高級語言中的數組名、記錄名、檔案名稱等這些名字即標記,其實傳遞的是這個數據結構的地址;
數據耦合/數據耦合(data coupling):是指模組藉由傳入值共享數據,每一個數據都是最基本的數據,而且只分享這些數據(例如傳遞一個整數給計算平方根的函式)。
訊息耦合(message coupling,是無耦合之外,耦合度最低的耦合):可以藉由以下二個方式達成:狀態的去中心化(例如在對象中),組件間利用傳入值或訊息傳遞 (計算機科學)來通信。
無耦合:模組完全不和其他模組交換信息。
面向對象程式設計
子類耦合(subclass coupling):描述子類和父類別之間的關係,子類連結到父類別,但父類別沒有連結到子類。
時空耦合(temporal coupling):二個動作只因為同時間發生,就被包裝在一個模組中。
後來的研究提出了許多不同層面的耦合性,並且用來評估實務上各種的模組化法則的實施程度。
缺點
緊密耦合的系統在開發階段有以下的缺點:
一個模組的修改會產生漣漪效應,其他模組也需隨之修改。
由於模組之間的相依性,模組的組合會需要更多的精力及時間。
由於一個模組有許多的相依模組,模組的可復用性低。
1.一個模組的修改會產生漣漪效應,其他模組也需隨之修改。
2.由於模組之間的相依性,模組的組合會需要更多的精力及時間。
3.由於一個模組有許多的相依模組,模組的可復用性低。
改善方法
機能設計是一種可以降低耦合性的方法,此方法以機能性的角度設法限制各模組需負責的事務。在類別 A及 B之間,若有以下任何一種情形,會提高二者的耦合性:
•A有一個屬性是參考類別B(此屬性的形態為類別B)
•A調用對象B提供的服務
•A有一個方法會參考類別B(此方式會傳回一形態為類別B的物性)
•A是類別B的子類。
鬆散耦合是指二個彼此相關的模組,其中的接口是一個簡單而穩定的接口,且其接口和任一模組內部的實現方式無關。
像CORBA或組件對象模型等系統,允許一對象在不知道另一對象實現方式的情形下和另一對象互動。這類系統甚至允許一對象和用其他語言撰寫的對象進行互動。
耦合性和內聚性
耦合性和內聚性二個名詞常一起出現,用來表示一個理想模組需要有的特點,也就是低耦合性及高內聚性。耦合性著重於不同模組之間的相依性,而內聚性著重於一模組中不同功能之間的關係性。低內聚性表示一個模組中的各機能之間沒什麼關係,當模組擴充時常常會出現問題。
模組的耦合性
以下是一種計算模組耦合性的方法:
對於數據和控制流的耦合:
•d:輸入數據參數的個數
•c:輸入控制參數的個數
•d:輸出數據參數的個數
•c:輸出控制參數的個數
全域耦合:
•g:用來存儲數據的全域變數
•g:用來控制的全域變數
環境耦合:
•w:此模組調用的模組個數(扇出)
•r:調用此模組的模組個數(扇入)
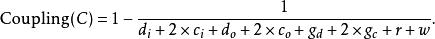 控制耦合
控制耦合若Coupling(C)數值越大,表示模組耦合的情形越嚴重,數值一般會界於0.67(低度耦合)到1.0(高度耦合)之間。
舉例,若一模組只有一個輸入數據參數,一個輸出數據參數:
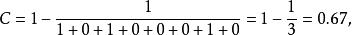 控制耦合
控制耦合若一模組的輸入數據參數、輸入控制參數、輸出數據參數及輸出控制參數都是5個,訪問10個全域變數,扇出和扇入的模組個數別是3個及4個:
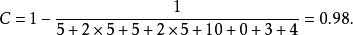 控制耦合
控制耦合相關條目
•相依性地獄
•傳出耦合
•內聚力 (計算機科學)
•面向對象程式設計用語列表
•make
•靜態程式分析
•控制反轉
•鬆散耦合