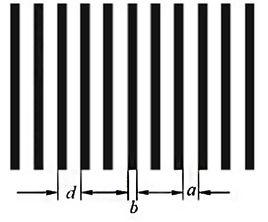
定義
能對入射光波振幅進行調製的衍射光柵稱為振幅光柵,又稱黑白光柵。
分類
矩形光柵
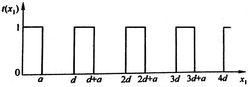 矩形光柵透射係數
矩形光柵透射係數由大量狹縫組成的透射光柵,如果考慮它的透射係數在光柵面上的變化,可以用右圖所示的曲線表示。由於這種光柵對入射光波振幅的調製是按矩形函式變化的,所以把這種光柵稱為矩形(振幅)光柵。
正弦光柵
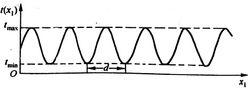 正弦光柵透射係數
正弦光柵透射係數相應地,透射係數按餘弦或者正弦函式變化的光柵稱為正弦(振幅)光柵,如右圖所示。雙光束干涉圖樣的強度分布函式具有餘弦函式的形式,因此把一張記錄了雙光束干涉條紋的底片進行“線性沖洗”後,它的透射係數分布就具有餘弦形式,這樣的一張底片就是一塊正弦光柵。
 振幅光柵
振幅光柵 振幅光柵
振幅光柵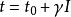 振幅光柵
振幅光柵 振幅光柵
振幅光柵 振幅光柵
振幅光柵所謂線性沖洗,就是沖洗後底片的透射係數 與底片原來記錄的光強度 有如下線性關係: ,式中 和 為常數。
強度分布
正弦光柵的夫琅禾費衍射圖樣
 振幅光柵
振幅光柵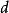 振幅光柵
振幅光柵 振幅光柵
振幅光柵假設正弦光柵包含有 個干涉條紋,條紋間距為 。那么,當單位振幅的單色平面波垂直照明光柵時,在光柵後緊靠著光柵的平面上的振幅分布可以寫成(設光柵透射係數沿 方向變化)
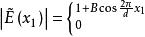 振幅光柵
振幅光柵 振幅光柵
振幅光柵該式記為式(1),其中,上式表示在光柵範圍內,下式表示在光柵範圍外, 是一個小於1的常數。
 振幅光柵
振幅光柵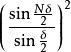 振幅光柵
振幅光柵求這類 個單元(每一個條紋可看做一個衍射單元)的光柵的衍射強度分布。只需求出單元的衍射因子,再把它乘上多光束干涉因子 便可以得到。對於所討論的正弦光柵,單位衍射產生的復振幅為
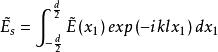 振幅光柵
振幅光柵該式記為式(2),其中略去了積分號前的常係數和二次相位因子,它們對所求的強度分布沒有影響。將式(1)代入式(2),得到
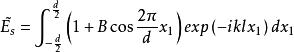 振幅光柵
振幅光柵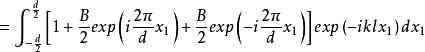 振幅光柵
振幅光柵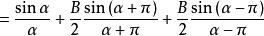 振幅光柵
振幅光柵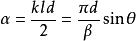 振幅光柵
振幅光柵 振幅光柵
振幅光柵其中 , 為光波波長。所以,正弦光柵衍射圖樣的強度分布為
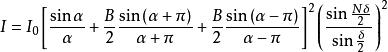 振幅光柵
振幅光柵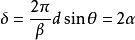 振幅光柵
振幅光柵注意到 ,故上式又可以寫為
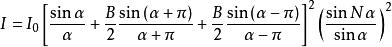 振幅光柵
振幅光柵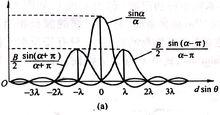 振幅光柵
振幅光柵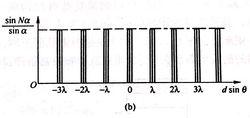 振幅光柵
振幅光柵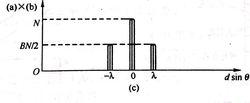 正弦光柵衍射的振幅分布
正弦光柵衍射的振幅分布 振幅光柵
振幅光柵 振幅光柵
振幅光柵