定義
拓撲關係是指圖形元素之間相互空間上的連線、鄰接關係並不考慮具體位置。這種拓撲關係是由數位化的點、線、面數據形成的以用戶的查詢或套用分析要求進行圖形選取、疊合、合併等
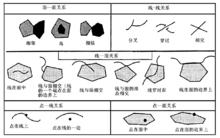拓撲關係（拓撲鄰接、拓撲關聯、拓撲包含）操作。建立空間要素之間的拓撲關係屬於地圖整飾。
點、線、面等實體之間的空間聯繫，如連通性、鄰接性、包含關係等。連通性是指對線段連線關係的判別;可以用在每個結點上匯集的線段的列表來表示。鄰接性通常指多邊形之間的鄰接關係；包含關係通常指多邊形包含點或包含其他的多邊形。
拓撲
是將各種物體的位置表示成 抽象位置。 在網路中，拓撲形象地描述了網路的安排和配置，包括各種結點和結點的相互關係。拓撲不關心事物的細節也不在乎什麼相互的比例關係，只將討論範圍內的 事物之間的相互關係表示出來，將 這些事物之間的關係通過圖表示出來。
類別
非拓撲屬性
兩點之間的距離； 一個點指向另一個點的方向；弧段的長度；一個區域的周長；一個區域的面積。
拓撲屬性
一個點在一個弧段的端點； 一個簡單弧段不會自相交； 一個點在一個區域的邊界上；一個點在一個區域的內部； 一個點在一個區域的外部； 一個點在一個環的內部； 一個簡單面是一個連續的面 。
拓撲數據結構
1.拓撲結構的基本元素
①拓撲線段（arc）
該線段中間不與其它線段存在聯繫。
②結點(node）
拓撲線段的兩個端點，分別為首結點、尾結點
③多邊形（poly）
由數條拓撲線段連線而成
拓撲數據舉例：
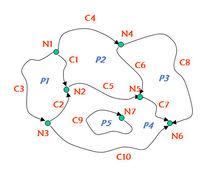拓撲數據舉例
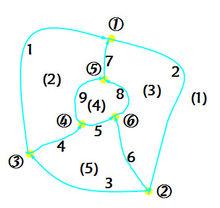拓撲關係2.拓撲關係表的建立
結點編碼：①②③④⑤⑥
線段編碼：1 2 3 4 5 6 7 8 9
多邊形編碼：(1)(2)(3)(4)(5)
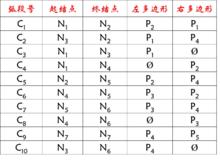拓撲關係常見拓撲結構
星型結構
星型結構是以一個節點為中心的處理系統，各種類型的入網機器均與該中心節點有物理鏈路直接相連。
星型結構的優點是結構簡單、建網容易、控制相對簡單。其缺點是屬集中控制，主節點負載過重，可靠性低，通信線路利用率低。
匯流排結構
匯流排結構是比較普遍採用的一種方式，它將所有的入網計算機均接入到一條通信線上，為防止信號反射，一般在匯流排兩端連有終結器匹配線路阻抗。
匯流排結構的優點是信道利用率較高，結構簡單，價格相對便宜。缺點是同一時刻只能有兩個網路節點相互通信，網路延伸距離有限，網路容納節點數有限。在匯流排上只要有一個點出現連線問題，會影響整個網路的正常運行。目前在區域網路中多採用此種結構。
環型結構
環型結構是將各台連網的計算機用通信線路連線成一個閉合的環。
環型拓撲是一個點到點的環型結構。每台設備都直接連到環上，或通過一個接口設備和分支電纜連到環上。 在初始安裝時，環型拓撲網路比較簡單。隨著網上節點的增加，重新配置的難度也增加，對環的最大長度和環上設備總數有限制。可以很容易地找到電纜的故障點。受故障影響的設備範圍大，在單環系統上出現的任何錯誤，都會影響網上的所有設備。
樹型結構
星型網路拓撲結構的一種擴充便是星行樹,如左圖所示。每個Hub與端用戶的連線仍為星型,Hub的級連而形成樹。然而,應當指出,Hub級連的個數是有限制的,並隨廠商的不同而有變化。
樹型結構是分級的集中控制式網路，與星型相比，它的通信線路總長度短，成本較低，節點易於擴充，尋找路徑比較方便，但除了葉節點及其相連的線路外，任一節點或其相連的線路故障都會使系統受到影響。
適用場合：只適用於低速、不用阻抗控制的信號，比如在沒有電源層的情況下，電源的布線就可以採用這種拓撲。
網狀結構
網狀結構分為全連線網狀和不完全連線網狀兩種形式。全連線網狀中，每一個節點和網中其它節點均有鏈路連線。不完全連線網中，兩節點之間不一定有直接鏈路連線，它們之間的通信，依靠其它節點轉接。這種網路的優點是節點間路徑多，碰撞和阻塞可大大減少，局部的故障不會影響整個網路的正常工作，可靠性高；網路擴充和主機入網比較靈活、簡單。但這種網路關係複雜，建網不易，網路控制機制複雜。廣域網中一般用不完全連線網狀結構。
混合型拓撲
就是兩種或兩種以上的拓撲結構同時使用。
優點：可以對網路的基本拓撲取長補短。 缺點：網路配置難度大。
蜂窩拓撲結構
蜂窩拓撲結構是無線區域網路中常用的結構。它以無線傳輸介質（微波、衛星、紅外等）點到點和多點傳輸為特徵，是一種無線網，適用於城市網、校園網、企業網。
由來
哥尼斯堡七橋問題摺疊
在數學上，關於哥尼斯堡七橋問題、多面體歐拉定理、四色問題等都是拓撲學發展史的重要問題。哥尼斯堡七橋問題哥尼斯堡（今俄羅斯加里寧格勒）是東普魯士的首都，普萊格爾河橫貫其中。十八世紀在這條河上建有七座橋，將河中間的兩個島和河岸聯結起來。人們閒暇時經常在這上邊散步，一天有人提出：能不能每座橋都只走一遍，最後又回到原來的位置。這個看起來很簡單又很有趣的問題吸引了大家，很多人在嘗試各種各樣的走法，但誰也沒有做到。看來要得到一個明確、理想的答案還不那么容易。
1736年，有人帶著這個問題找到了當時的大數學家歐拉，歐拉經過一番思考，很快就用一種獨特的方法給出了解答。歐拉把這個問題首先簡化，他把兩座小島和河的兩岸分別看作四個點，而把七座橋看作這四個點之間的連線。那么這個問題就簡化成，能不能用一筆就把這個圖形畫出來。經過進一步的分析，歐拉得出結論——不可能每座橋都走一遍，最後回到原來的位置。並且給出了所有能夠一筆畫出來的圖形所應具有的條件。這是拓撲學的“先聲”。
多面體的歐拉定理摺疊
在拓撲學的發展歷史中，還有一個著名而且重要的關於多面體的定理也和歐拉有關。這個定理內容是：如果一個凸多面體的頂點數是v、棱數是e、面數是f，那么它們總有這樣的關係：f+v-e=2。
根據多面體的歐拉定理，可以得出這樣一個有趣的事實：只存在五種正多面體。
它們是正四面體、正六面體、正八面體、正十二面體、正二十面體。
四色猜想摺疊
著名的“四色問題”也是與拓撲學發展有關的問題。四色問題又稱四色猜想，是世界近代三大數學難題之一。 四色猜想的提出來自英國。1852年，畢業於倫敦大學的弗南西斯·格思里來到一家科研單位搞地圖著色工作時，發現了一種有趣的現象：“看來，每幅地圖都可以用四種顏色著色，使得有共同邊界的國家都被著上不同的顏色。”
1872年，英國當時最著名的數學家凱利正式向倫敦數學學會提出了這個問題，於是四色猜想成了世界數學界關注的問題。世界上許多一流的數學家都紛紛參加了四色猜想的大會戰。1878～1880年兩年間，著名律師兼數學家肯普和泰勒兩人分別提交了證明四色猜想的論文，宣布證明了四色定理。但後來數學家赫伍德以自己的精確計算指出肯普的證明是錯誤的。不久，泰勒的證明也被人們否定了。於是，人們開始認識到，這個貌似容易的題目，其實是一個可與費馬猜想相媲美的難題。
進入20世紀以來，科學家們對四色猜想的證明基本上是按照肯普的想法在進行。電子計算機問世以後，由於演算速度迅速提高，加之人機對話的出現，大大加快了對四色猜想證明的進程。1976年，美國數學家阿佩爾與哈肯在美國伊利諾斯大學的兩台不同的電子計算機上，用了1200個小時，作了100億次判斷，終於完成了四色定理的證明。不過不少數學家並不滿足於計算機取得的成就，他們認為應該有一種簡捷明快的書面證明方法。
上面的幾個例子所講的都是一些和幾何圖形有關的問題，但這些問題又與傳統的幾何學不同，而是一些新的幾何概念。這些就是“拓撲學”的先聲。
