基本介紹
積分的概念可從不同的觀點出發向各種不同的方向抽象化。它大致可以分為兩個方向,一個方向是對取值於局部凸拓撲線性空間(不一定是數空間)的函式或測度定義積分(簡稱為在拓撲線性空間上的積分),另外一個方向是把和序關係有關的積分抽象化。下面對各方向取其有代表性的兩個積分予以敘述。
拓撲線性空間上的積分
 抽象積分
抽象積分 抽象積分
抽象積分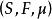 抽象積分
抽象積分拓撲線性空間上的積分(Bochner積分)設為定義在有限測度空間上,取值於Banach空間X中的函式,如果在使
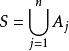 抽象積分
抽象積分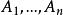 抽象積分
抽象積分 抽象積分
抽象積分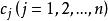 抽象積分
抽象積分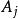 抽象積分
抽象積分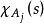 抽象積分
抽象積分的互不相交的F可測集上,x(s)分別取常量,就稱它為 階梯函式(step function)或 有限值函式(finite-valued function)。使用的定義函式,可以把這個階梯函式表示為
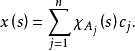 抽象積分
抽象積分 抽象積分
抽象積分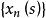 抽象積分
抽象積分如果對於能選取適當的階梯函式序列,使得在S上對幾乎一切s,
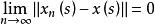 抽象積分
抽象積分 抽象積分
抽象積分 抽象積分
抽象積分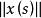 抽象積分
抽象積分 抽象積分
抽象積分 抽象積分
抽象積分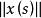 抽象積分
抽象積分 抽象積分
抽象積分成立,則稱為 強可測的(strongly measurable)。當為強可測,且作為S上的實值函式為Lebesgue可積時,則定義為 Bochner可積的(Bochner integrable)(由的強可測性可以得到的可測性)。特別當是Bochner可積的階梯函式
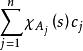 抽象積分
抽象積分時,其Bochner積分定義為
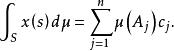 抽象積分
抽象積分 抽象積分
抽象積分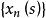 抽象積分
抽象積分一般地說,對於Bochner可積函式,可以證明,存在滿足下列條件的Bochner可積的階梯函式序列:
i)對幾乎一切S,
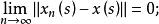 抽象積分
抽象積分ii)
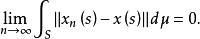 抽象積分
抽象積分 抽象積分
抽象積分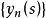 抽象積分
抽象積分 抽象積分
抽象積分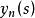 抽象積分
抽象積分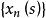 抽象積分
抽象積分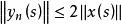 抽象積分
抽象積分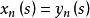 抽象積分
抽象積分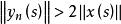 抽象積分
抽象積分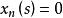 抽象積分
抽象積分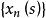 抽象積分
抽象積分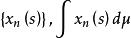 抽象積分
抽象積分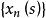 抽象積分
抽象積分 抽象積分
抽象積分(例如,由的強可測性得到,存在階梯函式序列,對幾乎一切s,它強收斂於,對此,如下地定義階梯函式序列:當時,令;當時,令;則滿足上述條件i),ii)。)從而對於這樣的強收斂,且其極限不依賴於的選擇方法。而的Bochner積分(Bochner integral),就定義為
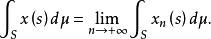 抽象積分
抽象積分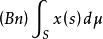 抽象積分
抽象積分 抽象積分
抽象積分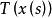 抽象積分
抽象積分為了和其他積分加以區別,有時把Bochner積分寫作。Bochner可積函式在任意的F可測集上都是Bochner可積的,除此之外,Lebesgue積分的幾乎所有性質(線性,完全可加性,絕對連續性,Lebesgue收斂定理,Fubini定理等),把絕對值換以範數之後都照樣成立。但是Radon-Nikodym定理不成立。當T是由Banach空間X到Banach空間Y的連續線性運算元時,若S上取值於X中的函式是Bochner可積的,則作為S上取值於Y中的函式是Bochner可積的,且
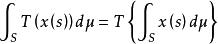 抽象積分
抽象積分成立。特別當S是n維Euclid空間時,Bochner積分具有強可微性 。
Birkhoff積分
 抽象積分
抽象積分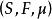 抽象積分
抽象積分 抽象積分
抽象積分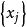 抽象積分
抽象積分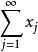 抽象積分
抽象積分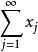 抽象積分
抽象積分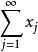 抽象積分
抽象積分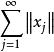 抽象積分
抽象積分Birkhoff積分是關於在有限測度空間上定義的,在Banach空間X中取值的函式,按Lebesgue積分的構造方法定義的積分。首先,對於X的元的可列族,當級數在其各項的次序任意改變之後仍然強收斂時,稱為無條件收斂(unconditionally converge)。當無條件收斂時,可以證明,它的和不依賴於相加的順序,總是一定的。特別當X是數空間時,無條件收斂和絕對收斂的概念是一致的;但一般地說,無條件收斂的級數並不一定絕對收斂(絕對收斂是指收斂)。給定S的一個可列分割
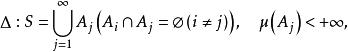 抽象積分
抽象積分 抽象積分
抽象積分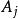 抽象積分
抽象積分若函式在每個上有界且
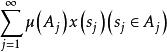 抽象積分
抽象積分 抽象積分
抽象積分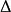 抽象積分
抽象積分無條件收斂,則稱關於可求和,此種和的全體
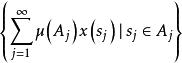 抽象積分
抽象積分 抽象積分
抽象積分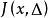 抽象積分
抽象積分 抽象積分
抽象積分 抽象積分
抽象積分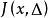 抽象積分
抽象積分 抽象積分
抽象積分 抽象積分
抽象積分 抽象積分
抽象積分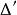 抽象積分
抽象積分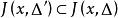 抽象積分
抽象積分 抽象積分
抽象積分的凸閉包,稱為對於△的 積分值域(integral range),記作。於是,如果對任意的正數,可選取S的可列分割△,使關於△可求和,且的直徑小於,則稱為 Birkhoff可積的(Birkhoff integrable)。若關於某一可列分割△可求和,則可以證明,它對△的任一加細仍然是可求和的,且。從而當是Birkhoff可積時,
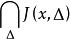 抽象積分
抽象積分成為只含有X的一個點的集合。此
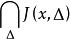 抽象積分
抽象積分 抽象積分
抽象積分定義為的 Birkhoff積分(Birkhoff integral),寫作
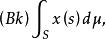 抽象積分
抽象積分或簡寫為
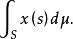 抽象積分
抽象積分Birkhoff可積函式在任意的F可測子集上仍為Birkhoff可積函式。Birkhoff積分作為集函式具有完全可加性和絕對連續性,對於被積函式具有線性性質。但Fubini定理不成立。又對於收斂定理來說不能得到Bochner積分那樣好的結果,Bochner可積函式必是Birkhoff可積的,但其逆不成立。
以此Birkhoff積分的構造法為基礎,G.Birkhoff和R.S.Phillips對取值於局部凸拓撲線性空間中的函式的積分作了定義。用此種積分的理論,使得Birkhoff積分成為這種積分基於在Banach空間上引人拓撲的方法,不同而得到的特殊情形。 進一步C.E.Rickart把Birkhoff積分推廣到取值為局部凸拓撲線性空間的子集的函式,並求得了Radon-Nikodym定理 。

