簡介
由無理數引發的數學危機一直延續到19世紀。直到1872年,德國數學家戴德金從連續性的要求出發,用有理數的“分割”來定義無理數,並把實數理論建立在嚴格的科學基礎上,才結束了無理數被認為“無理”的時代,也結束了持續2000多年的數學史上的第一次大危機。
概述
戴德金分割,是將一切有理數的集合劃分為兩個非空且不相交的子集A和A',使得集合A中的每一個元素小於集合A'中的每一個元素。集合A稱為劃分的下組,集合A'稱為劃分的上組,並將這種劃分記成A|A'。戴德金把這個劃分定義為有理數的一個分割。(有些分割是有理數產生的,在這樣的分割中,要么有最大元素,要么有最小元素,但有些分割卻不是)。
案例
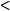 戴德金分割
戴德金分割例1 一切滿足不等式a 1的有理數a,歸入下組集合A中,一切滿足a' 1的a',歸入上組集合A'中。
則得出一個分劃。在這種分劃中,數1屬於A',且顯然成為其中最小的數。而在A組內並無最大數。
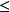 戴德金分割
戴德金分割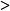 戴德金分割
戴德金分割例2 一切滿足不等式a 1的有理數歸入下組集合A中,一切滿足a' 1的有理數a',歸入上組A'中。
則同樣得出一個分劃。在這種分劃中,上組無最小數,而在下組中有最大數1。
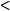 戴德金分割
戴德金分割 戴德金分割
戴德金分割例3 取使得a^2 2的一切正有理數a,數0及一切負有理數歸入下組集合A中,使a'^2 2的一切正有理數a'歸入上組集合A'中。
以上得出了有理數的僅有的三種類型的分劃,即:
(1)在下組A內無最大數,而在上組A'內有最小數r;
(2)在下組A內有最大數r,而在上組A'內無最小數;
(3)在下組A內既無最大數,在上組A'內也無最小數。
在前兩種情形,稱分劃由有理數r產生,(r稱為A與A'之間的界數),又或說分劃定義有理數r,在例1,2中,1便是這樣的數。
而在第三種情形中,界數並不存在,分劃並不定義任何有理數。於是引入相對於有理數的新的對象——無理數,並約定任一由第(3)類型的分劃定義某一無理數α。這個數α便代替缺少的界數。把界數α插入在A組的一切數a與A'組的一切數a'中間。在例3中,這個相對於有理數的新創的數即是根號2。對於這種劃分,每當考慮一個不是由有理數產生的分割時,就得到一個新數,即無理數,並認為這個數是由這種分割完全確定的。
戴德金把這種劃分定義為有理數的一個分割,記為A|A'。因為不存在有理數a使得a的平方等於2(見附註1),戴德金說,考慮一個不是由有理數產生的分割A|A'時,就得到一個新數,即無理數α,這個數是由分割A|A'完全確定的。因此,戴德金就把一切實數組成的集合R定義為有理數集的一切分割,而一個實數α就是一個分割A|A'。在這一定義中,由一個給定的有理數r產生的兩個實質上等價的分割(視數r是A最大元素還是A'的最小元素而定)被看成是同一的。為了確定起見,可以約定:凡是說到確定有理數r的分劃時,常把這數放在上組內。
這樣,所有可能的分割構成了數軸上的每一個點,既有有理數,又有無理數,統稱實數。
在解析函式中,對實數的定義大意是,先從自然數出發定義正有理數,然後通過無窮多個有理數的集合來定義實數。
有理數及無理數總稱為實數。實數的概念,是數學分析的基本概念之一。
附註1:
在有理數域不存在有理數p/q(p/q為既約分數),使其平方等於2。
證明(反證法):
假設存在這樣的既約分數p/q,使其平方等於2,即有p^2=2q^2,所以p為偶數,記p=2r(其中r為整數),於是q為奇數。
將p=2r代入p^2=2q^2得q^2=2r^2,故q為偶數,但這與假設相矛盾,所以不存在有理數p/q,使其平方等於2。
成就及影響
 戴德金分割
戴德金分割戴德金的主要成就是在代數理論方面。他研究過任意域、環、群、結構及模等問題,並在授課時率先引入了環(域)的概念,並給理想子環下了一般定義,提出了能和自己的真子集建立一對應的集合是無窮集的思想。在研究理想子環理論過程中,他將序集(置換群)的概念用抽象群的概念來取代,並且用一種比較普通的公式(戴德金分割概念)表示出來,比康托爾的公式要簡化得多,並直接影響了後來皮亞諾的自然數公理的誕生。是最早對實數理論提出了許多論據的數學家之一。
戴德金在數學上有很多新發現。不少概念和定理以他的名字命名。他的主要貢獻有以下兩個方面:在實數和連續性理論方面,他提出“戴德金分割”,給出了無理數及連續性的純算術的定義。

