概述
心智量化模型由羅嘯於倫敦大學學院(UCL)就讀期間在相關的論文中首次提出。基於其在信號系統方面的研究,他在論文中第一次提出了心智也是可以進行量化的,而保持這個模型穩定的基礎就是信號系統中的無限脈衝回響(IIR)系統。在IIR系統中,有限信號的輸入可能會產生無限長的信號輸出,需要依據Z變換之後的極點是否在複數坐標的單位圓內來判斷系統是否穩定。通過分析,羅嘯證明了將IIR的系統架構運用在一些抽象參數的量化上是可以行的,整個模型在經過Z變換之後具有穩定性,藉此提出了將消費者心智資源進行量化的分析模型。模型理論
與信號系統的類比
在信號系統中,最基礎的信號單位為比特,依據不同的實際需求,信號系統工作者會在設計系統時構建出擁有不同邏輯體系的系統。基礎信號在系統之間經過運算之後產生變化,最終由輸入信號變為輸出信號。系統的構建與運算
之後,依靠IIR系統的強健性,用該系統的反饋邏輯來保證各個運算元之間邏輯關係的穩定性。同時在各個運算元內部以及各個比特屬性之間,依舊用IIR系統的基礎構架來保證他們之間邏輯關係的穩定性,從而使整個模型系統趨於穩定。
消費傾向參數(Propensity)
在整個模型中,量化的最終體現為消費傾向參數(Propensity),他具有如下屬性:1. It’s about the will that people want to buy the product.(它代表了消費者的消費傾向)
2. It’s abstract but the main parameter in this modeling approach. (它是抽象的,但同時是這個模型中最為關鍵的參數)
3. In this project, the propensity is quantified as the feedback to connect the business IR systems in different product cycles.(我們用該參數來連結不同商業運算元所形成的脈衝回響系統。)
4. It is initialized by a Gaussian distribution with 97% energy focused on the interval of [-10, 10]. .(在初始假設中,消費傾向參數以高斯分布來進行初始化。)
5. It will be changed in each business processor.(它會被各個不同的商業運算元所改變)
6. The final propensity is the only parameter which will affect whether people buy the product.(最終的消費傾向參數是關於單個消費者是否進行購買活動的唯一標準)
7. It can be regarded as the signal in telecom system. It will be modulated by the people, affected by the noise, get to the end of the system and generate the displayed result.(它類似於電信系統中的信號,由各個消費者進行內部調製,各個運算元模擬外部運算邏輯與噪音,在終端形成其最終的輸出信號)
模型的輸出結果
消費傾向分布(Propensity Distribution)
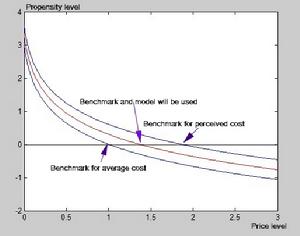
通過該模型最終形成量化的指標---消費傾向參數。將該參數的消費者分布用柱狀圖表示出來可以發現,其在大致形狀上形成一個左陡右緩的山體,且山體右端從頂峰向下的有明顯“陡---緩---陡---緩”的坡度變更,而購買行為的臨界閾值一般存在於分布的右端。截止到2014年,尚沒有標準的數學公式可以描述該分布,僅能通過計算機建模後得到。圖中所示的消費傾向分布皆為30000-40000人左右的消費傾向分布,更平滑的分布圖樣會需求更高計算能力的計算機來進行模擬。套用
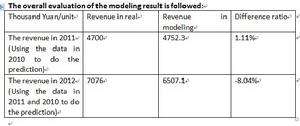
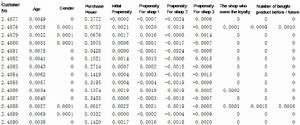
除了進行預測以外,該模型可以模擬區域內消費者包括消費傾向參數在內的多個參數,同時模擬整個商業活動中消費者購買決策的下達過程。其中蘊含的數據可以很好地支持包括年齡分類,產品定位,精細化行銷等多種商業手段。
