概念
循環模(cyclic module)是一類特殊的有限生成模。可由一個元素生成的A模M稱為循環模(A是有單位元環),即,有x∈M,使得M=Ax成立。環A作為A模是循環模。A模M是循環模的充分必要條件是MA/I,其中I為A的一個左理想。
模
模是一個重要的代數系統。它是一個帶運算元區A的交換(加)群M。給定集合A與交換群M,若定義了a∈A與x∈M的乘積ax∈M,並且這個積滿足條件:
1.a(x+y)=ax+ay (a∈A,x,y∈M),
則稱A為M的運算元區,稱M為帶運算元區A的模,又稱為A上的模或A模。這時,由對應(a,x)→ax確定的映射A×M→M,稱為A作用到M上的運算。任意a∈A可誘導出M的自同態a:x→ax,而考慮交換群M能否成為A模就是看能否給出映射
μ: A→End(M), a→a.
特別地,考慮A是結合環,若滿足上述條件1的A模還滿足:
2.(a+b)x=ax+bx;
3.(ab)x=a(bx);
即映射μ:A→End(M)為環同態,則稱M為左A模或左環模。由於A到M上的運算是寫在左側,所以M就稱為左A模,記為M。類似地,有右A模M,記為M。若A有單位元1,且又滿足條件
4.1x=x (x∈M);
則稱M為酉模或麼模。
模論
抽象代數學的重要組成部分之一,主要研究環上的模。模的概念本質上是域上向量空間的直接推廣。早在19世紀,狄利克雷(Dirichlet,P.G.L.)就曾經考慮過多項式環上的模,20世紀20年代,諾特(Noether,E.)曾一再提出過模的重要作用。交換環上的模在代數幾何中有重要作用,非交換環特別是群環上的模就是群的線性表示,域上的模就是向量空間.到了20世紀40年代,由於環論的需要和同調代數的興起,模論得到了進一步發展.近30年來,已成為同調代數、群論、環論、代數K理論、範疇論等分支學科研究中不可缺少的工具,並在其他數學分支,如代數幾何、拓撲學、泛函分析甚至微分方程等領域裡得到了較廣泛的套用.現代模論已成為內容豐富、文獻浩繁的代數學的一個獨立分支.
有限生成模
模論的基本概念之一。指可以表示出A模M中任一個元的M的一組元素。考慮環A模M時,A的元稱為純量,A稱為M的係數環或基環,運算A×M→M稱為純量乘法,ax稱為x的純量倍,它的全體記為Ax。對M的一簇元素{x},形式為:
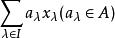 循環模
循環模的元的全體N是包含全部x(λ∈I)的M的最小子模,它等於和:
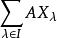 循環模
循環模稱N由{x}所生成,而{x}稱為N的生成系。若I是可數集,且M由{x}生成,則稱M為可數生成模。當I是有限集,且M=Ax+Ax+…+Ax,稱M為有限生成模,此時任x∈M有表示式:
x=rx+rx+…+rx, r,r,…,r∈A.
模M是有限生成若且唯若對M的每一個子模集{A|i∈I},若有:
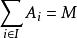 循環模
循環模則存在有限子集II,使得:
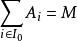 循環模
循環模環
對並與差運算封閉的集類,測度論中重要概念之一.設F是Ω上的一個非空集類.如果它對集的並及差運算封閉,即對任何A,B∈F,都有A∪B∈F,A\B∈F,則稱F為Ω上的環.例如,若F是由實直線R上任意有限個左開右閉的有限區間的並集:
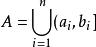 循環模
循環模的全體構成的集類,則F是R上的一個環。環也是對於交與對稱差運算封閉的集類,並按這兩種運算成為布爾環(參見第一卷《布爾代數》)。要把R上的勒貝格測度和勒貝格-斯蒂爾傑斯測度以及相應的積分理論推廣到更一般的集合上,就需要做一系列奠基工作,其中之一是建立一些特殊的集類並研究其性質。環以及半環、σ環、代數、σ代數等重要集類正是為了這一目的而引入的。
