彌爾曼定理
例子1
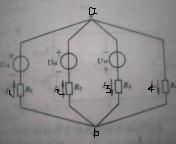
電路中,Us1與R1串聯,Us2與R2串聯,Us4與R4串聯,它們與R3電阻組成並聯電路.即Us1與R1串聯後,並聯Us2與R2的串聯,再並聯Us4與R4的串聯,再並聯R3。
可知,電路中兩節點分別為1和0(地),
那么,U10=A/B,其中:A=Us1/R1+Us2/R2+Us4/R4,B=G1+G2+G3+G4,G為電導。計算式中會涉及到電流的方向問題,A中數值是正或負,就是看電流方向是正是反來確定的.
例子2
如果將例1中的"Us4與R4串聯"改為"電阻R與電流源Is串聯",那么,U10=A/B
其中:A=Us1/R1+Us2/R2+Is,B=G1+G2+G3,G為電導。
例子3
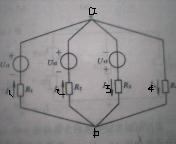
電路只有兩個節點,各條支路都跨接在這兩個節點之間。在已知電源電壓和電阻的情況下,若能求出兩個節點之間的電壓,那么各支路電流的計算便很容易解決了。
I1=(U1-Uab)/R1
I2=(U2-Uab)/R2
I3=(U3-Uab)/R3
I4=Uab/R4
 彌爾曼定理
彌爾曼定理而對節點a又可寫成 I1+I2-I3-I4=0
代上式得 (U1-Uab)/R1 +(U2-Uab)/R2 - (U3-Uab)/R3 - Uab/R4 = 0
整理後得到 Uab=U1/R1+U2/R2-U3/R3 / 1/R1+1/R2+1/R3+1/R4
上式就是計算節點電壓的公式,分母為各支路電阻倒數之和,恆為正.分子為各含源支路的電壓源電壓和該支路電阻的比值之代數和,當電壓源電壓的參考方向和節點電壓的參考方向一致時,取正號,反之取負號,這就是彌爾曼定理。