振動分析主要是考察系統對激勵的回響。周期激勵是一種典型的經常性激勵。由於周期激勵總可分解為若干個諧和激勵之和，故根據疊加原理，只要求出系統對各個諧和激勵的回響，再把它們疊加起來，就可得到系統對周期激勵的總回響。單自由度帶阻尼的系統在諧和激勵
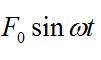強迫振動的作用下，運動微分方程可寫作：
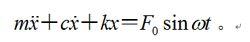強迫振動其回響是兩部分的和，一部分是阻尼振動的回響，這部分隨時間增大而迅速衰減；另一部分受迫振動的回響可寫作：
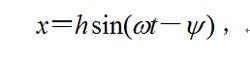強迫振動
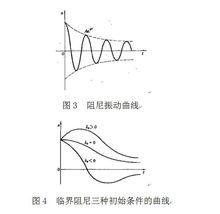強迫振動式中
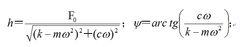強迫振動h/ F= H（），為定常回響振幅與激勵振幅之比，表征幅頻特性，或稱增益函式； ψ為定常回響和激勵的相位差，表征相頻特性。它們與激勵頻率
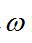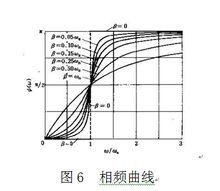
強迫振動的關係見圖5和圖6。
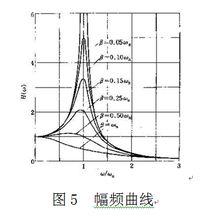
從幅頻曲線（圖5）可以看出，在小阻尼情況下，幅頻曲線具有單峰；阻尼愈小，峰愈陡；對應於峰頂的頻率稱為系統的共振頻率。在小阻尼情況，共振頻率與固有頻率差別不大。當激振頻率與固有頻率接近時，振幅急劇增加，這種現象稱為共振（諧振）。在共振時，系統的增益取極大值，即受迫振動最為激烈。故在一般情形下，總是力求避免出現共振，除非某些儀器與設備要利用共振來取得大幅度振動。
強迫振動從相頻曲線（圖6）可以看出，不論阻尼大小，在 ω處，相位差 ψ=π/2，這一特點可有效地用於共振測量。
除了定常激勵外，系統有時還會遇到非定常激勵。它大致可以分為兩類：一是突發性的衝擊作用。二是任意性的持久作用。在非定常激勵下，系統的回響也是非定常的。
分析非定常振動的一個有力工具是脈衝回響法。它用系統的單位脈衝輸入的瞬態回響描述系統的動態特性。單位脈衝可以用δ函式表示。在工程上，δ函式常定義為：
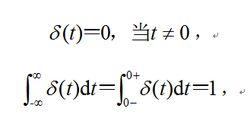強迫振動式中0表示 t軸上從左邊趨於零的點；0表示從右邊趨於0的點。
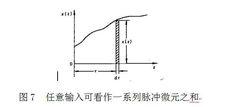強迫振動
強迫振動系統對應於在 t=0時作用的單位脈衝所產生的回響 h( t)，稱為脈衝回響函式。假定系統在脈衝作用之前是靜止的，則當 t<0時，有 h( t)=0。知道系統的脈衝回響函式，就可以求系統對任意輸入 x( t)的回響。這時，可以把 x( t)看作一系列脈衝微元
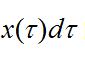強迫振動的和（圖7）。
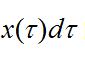強迫振動相當於在
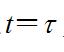強迫振動時作用的一個脈衝，系統對應於它的回響為：
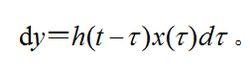強迫振動基於疊加原理，系統對應於 x( t)的總回響為：
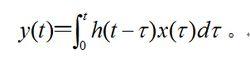強迫振動這一積分稱為褶積積分或疊加積分。
