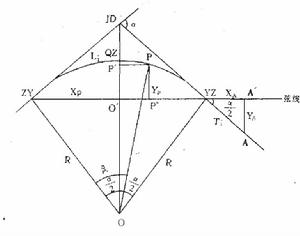
概念
弦線支距法是指以圓曲線的弦為X軸，弦的垂線為Y軸，以每段的起點為原點，計算曲線上各點的坐標值，在實地測設曲線的方法。
有如下特點：
（1）計算簡便：曲線支距可在國標參考表中查出，或以計算尺按拋物線插入法求出。一切計算工作均可在現場立即進行。
（2）測設方法簡便：安置儀器的站數較少，只瞄方向，不調角度，標明支距數後測量工作即可開展。測設曲線大多在定切線後返回儀器途中完成。
（3）容易檢查，不易發生錯誤，精度高：曲線由兩端向中間測設，支距由儀器瞄準，誤差不累積等均使測設曲線精度大為提高，檢查方法簡單，有錯誤立即發現糾正。
弦線支距法在地下工程施工測量中的套用探討
內容簡介
地下工程平面線型設計中，往往圓曲線和帶有緩和曲線的圓曲線總長所占的比重比直線總長大。在許多地下工程隧道施工掘進過程中，測設曲線常用的方法有切線支距法、控線偏距法、弦線支距法，經過各種地下工程施工測量的長期實踐，弦線支距法是測設曲線最適用而且運用範圍有待於進一步推廣的一種測沒曲線的方法。
曲線測量實例
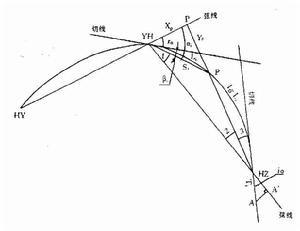緩和曲線的弦線求支距示意圈地下鐵道和其它各種地下工程施工日益增多，曲線隧道在開挖過程中 需要隨時提供方向線。為了在施工中滿足施工工藝的要求和節約人力、物力等，採用雷射指向儀指向，弦線支距法公式計算弦長和支距值，雷射指向儀配合水平尺，結合弦長和支距值即可指導曲線隧道的測設和施工。
線支距法公式是在工程實踐需要的基礎上推導出來的，用PCI500機和BASIC語言編程或用CASIO、fx--4800P計算器編程來計算弦長和支距值，速度快且採用整套嚴密公式計算精度高。弦線支距法由於其適應面廣，支距值精確且小，便於量距測設和施工，測設精度高、誤差不積累等優點。在工程實踐中正得到普遍重視和廣泛套用，如北京捷運西東和東王區間，深圳捷運車竹區間，天東站一、二層聯絡通道和曲線出入口通道，以及曲線過街道和各類地下暗挖管線等。
實際工作中，根據曲線的設計情況和開挖豎井及掌子面的位置情況，靈活運用公式，並且注意公式中符號的意義，建立起整套的弦長和支距值內業資料，雷射指向儀指出弦線的方向和坡度，根據弦長量出對應的支距值來定出曲線隧道架設鋼格柵的中線點。弦線支距法公式思路明確並經工程實踐驗證，同樣也適用於各種設計參數的山嶺隧道曲線測設中。彌補和豐富了曲線隧道掘進過程中曲線測設方法的不足，有普遍的推廣價值。
弦線支距法在曲線隧道施工測量中的套用
曲線隧道測設方案的比選
線上路測量中，曲線測量是比較複雜而又非常重要的一項工作，長期以來，測設曲線一直採用偏角法和切線支距法。其中偏角法較為普遍，優點是易校核，適用於山區及平原地區；缺點是誤差積累。切線支距法方法簡單，誤差不積累；缺點是不能發現中間點的測量錯誤，僅適用於平坦地區。
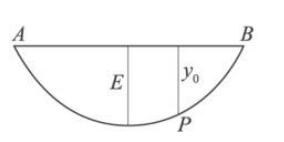圖1 弦線支距法求y0值示意提出一種新的曲線測設方法——弦線支距法。如圖1，把曲線 A、B之間的兩個端點用直線連線起來，以弦線AB為基準計算支距。不難看出，AB兩點支距都為0；曲線向前延伸，曲線上任一點P點的支距y將逐漸變大，大到一個極大值E為止再變小，最終為0，則支距y值始終在一個有上限值的範圍內變化。即弦線支距法以曲線的兩個端點連線而成的弦線為基準線，通過量取基準線上任一點支距(垂線)y，即可定出曲線。該方法簡單方便，且在雷射向儀的配合下，放樣數據十分精確。
弦線支距法的原理
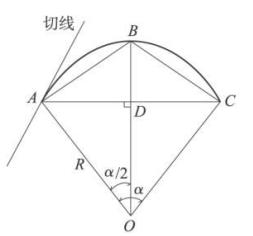圖2 弦線支距法原理計算示意以圓曲線為例，說明弦線支距法的原理。如圖2所示，根據等腰三角形 的角分線垂直平分對邊的幾何原理，利用三角函式關係，即可求任一點的支距值。假設以AC弦線為X軸，DB為y軸，實際測設中，把儀器支於A點，沿弦線方向量取x定出D點，於D點定出AC線的垂分線，在垂分線(y軸)上量取y即可定出圓弧上B點，依次類推測出其他點。
測設要點
在工程曲線所占比例較大時，在開挖過程中用雷射指向儀安置於弦線方向，根據計算好的各點量取對應弦長和支距值，指導曲線隧道架立鋼格柵、噴錨、襯砌、開挖等施工工藝。實踐表明，該方法具有支距短、誤差不積累、簡單、弦線和雷射指向儀變動次數少等優點，為暗挖隧道按時貫通爭取了時間，貫通誤差均小於規範允許的限差，值得在同類工程中推廣。
