簡介
最短路問題是網路最最佳化中一個基本而又非常重要的問題,這一問題相對比較簡單,在實際生產和生活中經常遇到,許多的網路最最佳化問題可以化為最短路問題,或者用最短路算法作為其子程式.因此,最短路的用途已遠遠超出其表面意義迄今為止,所有最短路算法都只對不含負迴路的網路有效,實際上對含有負迴路的網路,其最短路問題是NP困難的,因此本研究所討論的網路也不含負迴路.此外,如果將無向圖每條邊用兩條端點相同、方向相反的弧來代替,可以將其化為有向圖,因而不討論無向圖.本研究中未述及的術語、記號可參見文獻 。
Floyd算法是一種用於尋找給定加權圖中頂點間最短路徑的算法,以1978年圖靈獎獲得者史丹福大學計算機科學系教授RobertW.Floyd命名。Floyd算法採用動態規劃的原理計算兩兩頂點間最短路徑[3],主要解決網路路由尋找最優路徑的問題 。
算法思想
路徑矩陣
通過一個圖的權值矩陣求出它的每兩點間的最短路徑矩陣。
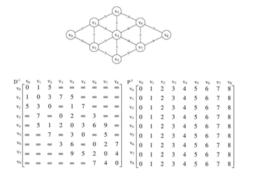
從圖的帶權鄰接矩陣A=[a(i,j)] n×n開始,遞歸地進行n次更新,即由矩陣D(0)=A,按一個公式,構造出矩陣D(1);又用同樣地公式由D(1)構造出D(2);……;最後又用同樣的公式由D(n-1)構造出矩陣D(n)。矩陣D(n)的i行j列元素便是i號頂點到j號頂點的最短路徑長度,稱D(n)為圖的距離矩陣,同時還可引入一個後繼節點矩陣path來記錄兩點間的最短路徑。
採用鬆弛技術(鬆弛操作),對在i和j之間的所有其他點進行一次鬆弛。所以時間複雜度為O(n^3);
狀態轉移方程
其狀態轉移方程如下:
map[i,j]:=min{map[i,k]+map[k,j],map[i,j]};
map[i,j]表示i到j的最短距離,K是窮舉i,j的斷點,map[n,n]初值應該為0,或者按照題目意思來做。
當然,如果這條路沒有通的話,還必須特殊處理,比如沒有map[i,k]這條路。
算法過程
1,從任意一條單邊路徑開始。所有兩點之間的距離是邊的權,如果兩點之間沒有邊相連,則權為無窮大。
2,對於每一對頂點 u 和 v,看看是否存在一個頂點 w 使得從 u 到 w 再到 v 比已知的路徑更短。如果是更新它。
把圖用鄰接矩陣G表示出來,如果從Vi到Vj有路可達,則G[i][j]=d,d表示該路的長度;否則G[i][j]=無窮大。定義一個矩陣D用來記錄所插入點的信息,D[i][j]表示從Vi到Vj需要經過的點,初始化D[i][j]=j。把各個頂點插入圖中,比較插點後的距離與原來的距離,G[i][j] = min( G[i][j], G[i][k]+G[k][j] ),如果G[i][j]的值變小,則D[i][j]=k。在G中包含有兩點之間最短道路的信息,而在D中則包含了最短通路徑的信息。
比如,要尋找從V5到V1的路徑。根據D,假如D(5,1)=3則說明從V5到V1經過V3,路徑為{V5,V3,V1},如果D(5,3)=3,說明V5與V3直接相連,如果D(3,1)=1,說明V3與V1直接相連。
複雜度
時間複雜度:O(n^3)
空間複雜度:O(n^2)