原理介紹
康托展開運算
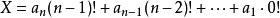 康托展開
康托展開 康托展開
康托展開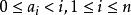 康托展開
康托展開其中, 為整數,並且 。
 康托展開
康托展開表示原數的第i位在當前未出現的元素中是排在第幾個
z康托展開的逆運算
既然康托展開是一個雙射,那么一定可以通過康托展開值求出原排列,即可以求出n的全排列中第x大排列。
如n=5,x=96時:
首先用96-1得到95,說明x之前有95個排列.(將此數本身減去1)用95去除4! 得到3餘23,說明有3個數比第1位小,所以第一位是4.用23去除3! 得到3餘5,說明有3個數比第2位小,所以是4,但是4已出現過,因此是5.用5去除2!得到2餘1,類似地,這一位是3.用1去除1!得到1餘0,這一位是2.最後一位只能是1.所以這個數是45321。
按以上方法可以得出通用的算法。
康托展開和逆康托展開
康托展開舉例
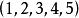 康托展開
康托展開再舉個例子說明。
在
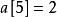 康托展開
康托展開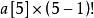 康托展開
康托展開首位是3,則小於3的數有兩個,為1和2,,則首位小於3的所有排列組合為
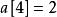 康托展開
康托展開第二位是4,由於第一位小於4,1、2、3中一定會有1個充當第一位,所以排在4之下的只剩2個,所以其實計算的是在第二位之後小於4的個數。因此。
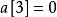 康托展開
康托展開第三位是1,則在其之後小於1的數有0個,所以。
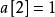 康托展開
康托展開第四位是5,則在其之後小於5的數有1個,為2,所以。
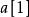 康托展開
康托展開最後一位就不用計算啦,因為在它之後已經沒有數了,所以固定為0
根據公式:
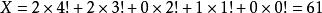 康托展開
康托展開所以比34152小的組合有61個,即34152是排第62。
代碼實現
逆康托展開舉例
 康托展開
康托展開一開始已經提過了,康托展開是一個全排列到一個自然數的雙射,因此是可逆的。即對於上述例子,在給出61可以算出起排列組合為34152。由上述的計算過程可以容易的逆推回來,具體過程如下:
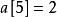 康托展開
康托展開用 61 / 4! = 2餘13,說明,說明比首位小的數有2個,所以首位為3。
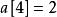 康托展開
康托展開用 13 / 3! = 2餘1,說明,說明在第二位之後小於第二位的數有2個,所以第二位為4。
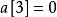 康托展開
康托展開用 1 / 2! = 0餘1,說明,說明在第三位之後沒有小於第三位的數,所以第三位為1。
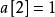 康托展開
康托展開用 1 / 1! = 1餘0,說明,說明在第二位之後小於第四位的數有1個,所以第四位為5。
最後一位自然就是剩下的數2。
通過以上分析,所求排列組合為 34152。
代碼實現
用途
顯然,n位(0~n-1)全排列後,其康托展開唯一且最大約為n!,因此可以由更小的空間來儲存這些排列。由公式可將X逆推出唯一的一個排列。

