簡要證明
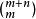 庫默爾定理
庫默爾定理組合數 所含p的冪次數為
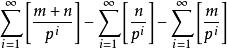 庫默爾定理
庫默爾定理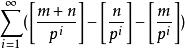 庫默爾定理
庫默爾定理=
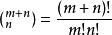 庫默爾定理
庫默爾定理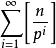 庫默爾定理
庫默爾定理這是因為組合數公式 以及n!含有素數p的冪次公式vp(n!)= 。
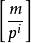 庫默爾定理
庫默爾定理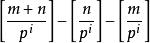 庫默爾定理
庫默爾定理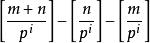 庫默爾定理
庫默爾定理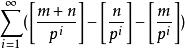 庫默爾定理
庫默爾定理對於某個p^i, 等於m在p進制表示下去掉後i位,在第i+1位上,m+n在這一位上進位的充要條件是 =1,不進位則 =0.因此 就是m+n在p進制下的進位次數。
套用舉例
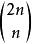 庫默爾定理
庫默爾定理例 (2014 CMO 30,4,21分)求具有下述性質的所有整數k:存在無窮多個正整數n,使得n+k不整除 。
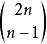 庫默爾定理
庫默爾定理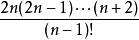 庫默爾定理
庫默爾定理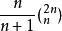 庫默爾定理
庫默爾定理解 ∵ = = ,
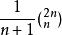 庫默爾定理
庫默爾定理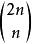 庫默爾定理
庫默爾定理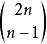 庫默爾定理
庫默爾定理∴ = - 是整數,
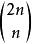 庫默爾定理
庫默爾定理∴n+1| 對任意正整數n成立,從而1不滿足要求。
當k≤0時,取n=p-k(p為奇素數,p>-2k),滿足要求。
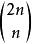 庫默爾定理
庫默爾定理當k≥2時,取k的一個素因子p,選取正整數m使得p^m>k,令n=p^m-k,我們證明:n+k不整除 。
顯然有n>0,由n<p^m知n在p進制下最多m位,∵p|k,p|p^m,∴p|n。∴在p+1進制下n個位為0.
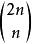 庫默爾定理
庫默爾定理∴2n=n+n最多進位m-1次。由庫默爾定理, 最多有m-1個p,∵n+k=p^m,∴
