定義
在空間坐標系內,平面的方程均可用三元一次方程Ax+By+Cz+D=0來表示。
類型
一、截距式
設平面方程為Ax+By+Cz+D=0,若D不等於0,取a=-D/A,b=-D/B,c=-D/C,則得平面的截距式方程: x/a+y/b+z/c=1
它與三坐標軸的交點分別為P(a,0,0),Q(0,b,0),R(0,0,c),其中,a,b,c依次稱為該平面在x,y,z軸上的截距。
二、點法式
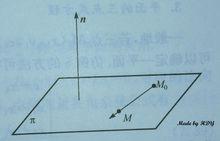 平面方程
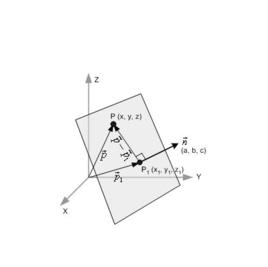
平面方程n為平面的法向量, n=(A,B,C),M,M'為平面上任意兩點, 則有n·MM'=0, MM'=(x-x0,y-y0,z-z0),從而得平面的點法式方程: A(x-x0)+B(y-y0)+C(z-z0)=0
三點求平面可以取向量積為法線
任一三元一次方程的圖形總是一個平面,其中x,y,z的係數就是該平面的一個法向量的坐標。
兩平面互相垂直相當於A1A2+B1B2+C1C2=0
兩平面平行或重合相當於A1/A2=B1/B2=C1/C2
點到平面的距離=abs(Ax0+By0+Cz0+D)/sqrt(A^2+B^2+C^2) 求解過程:面內外兩點連線在法向量上的映射Prj(小n)(帶箭頭P1P0)=數量積
三、一般式
Ax+By+Cz+D=0 ,其中A,B,C,D為已知常數,並且A,B,C不同時為零。
四、法線式
xcosα+ycosβ+zcosγ=p ,其中cosα、cosβ、cosγ是平面法矢量的方向餘弦,p為原點到平面的距離。