簡介
平方根法又叫Cholesky分解法，是求解對稱正定線性方程組最常用的方法之一。我們知道，對於一般方陣，為了消除LU分解的局限性和誤差的過分積累，而採用了選主元的方法。但對於對稱正定矩陣而言，選主元卻是完全不必要的。
定理及證明
設A為一n階對稱正定矩陣，即A滿足A^T=A且對任意的非零實係數向量z，都有z^TAz>0，則我們可以得出如下定理：Cholesky分解定理：若矩陣A對稱正定，則存在一對角元為正數的下三角陣L，使得
A=LL^T
上式中的L又稱為Cholesky因子。
證明：由於A對稱正定表明A的全部順序主子陣均正定，因此可知，存在一個單位下三角陣L'和一個上三角矩陣U，使A=L'U。令：
D=diag（u11,...,u1n）,U'=D^(-1)U，
則有
U'^TDL'^T=A^T=A=L'DU'，
從而
L'^TU'^(-1)=D^(-1)U'^(-T)L'D.
上式左邊是一個單位上三角矩陣，而右邊是一個下三角矩陣，故兩邊均為單位矩陣。於是，U'=L'^T，從而A=L'DL'^T。由此可知，D的對角元均為正數。令
L=L'diag(
,...,
),則A=LL^T，且L的對角元lii=
>0，i=1,...,n 證畢套用
若線性方程組Ax=b的係數矩陣是對稱正定的，我們可按如下的步驟求其解：1.求A的Cholesky分解：A=LL^T；
2.求解Ly=b得到y，
3.將y回代求解L^Tx=y得到x。
由以上定理的證明可知，Cholesky分解可用不選主元的Gauss消去法來實現。然而，更簡單而實用的方法是通過直接比較A=LL^T兩邊的對應元素來計算L。設L為一下三角形實矩陣，其元素由
（i為所在行，j為所在列）確定。比較A=LL^T兩邊對應的元素，得關係
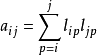
其中1
ijn首先，由
=
，得
=
.再由
=
，得=/，i=2,...,n.這樣便得到了矩陣L的第一列元素。假定已經算出L的前k-1列元素，由
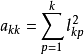
得
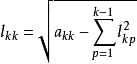
再由
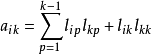
其中i=k+1,...,n.
得
其中i=k+1,...,n.
這樣便又求出了L的第k列元素。這種方法稱為平方根法。當然，亦可按行來逐次計算L。由於A的元素
被用來計算出
以後不再使用，所以可將L的元素存儲在A的對應位置上，這樣我們就得到如下算法。算法（正定矩陣的Cholesky分解）
for k=1 ：n
for i=1:k-1
a[k][k]-=a[k][i]*a[k][i]
end
a[k][k]=sqrt(a[k][k])
for i=k+1:n
for j=1:k-1
a[I][k]-=a[i][j]*a[k][j]
end
a[i][k]/=a[k][k];
end
end
由以上可知，用平方根算法解對稱正定線性方程組時，計算L的對角元素
需用到開方運算。為了避免開方，我們可求A之如下形式的分解A=LDL^T
其中L是單位下三角矩陣，D是對角均為正數的對角矩陣。這一分解稱作LDL^T分解，是Cholesky分解的變形。比較上式兩邊對應元素得
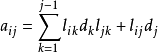
其中1
ijn.由此可確定
和
的計算公式如下：
其中k=1,...,j-1,
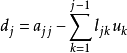
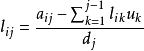
其中i=j+1,...,n.
這裡j=1,2,...,n.上述這種確定A的分解方法稱作改進的平方根方法。實際計算時，是將L的嚴格下三角元素存儲在A的對應位置上，而將D的對角元存儲在A的對應的對角位置上，這樣我們就得到如下的實用算法。
算法（計算LDL^T分解：改進的平方根法）
for(k=0;k<n;k++) {
for(i=0;i<k;i++)
a[k][k]-=a[i][i]*a[k][i]*a[k][i];
for(j=k+1;j<n;j++)
{
for(i=0;i<k;i++)
a[j][k]-=a[j][i]*a[i][i]*a[k][i];
a[j][k]/=a[k][k];
}
}
一旦求得A的LDL^T分解，只需再解如下兩個三角方程組
Ly=b和DL^Tx=y
即可求得線性方程組的解。利用這種方法求解對稱正定線性方程組所需的運算量僅是Gauss消去法的一半，而且還不需要選主元。此外，Cholesky分解的計算過程是穩定的。事實上，由關係式
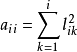
得
上式說明Cholesky分解中的量
能夠得以控制，因此其計算過程是穩定的。
