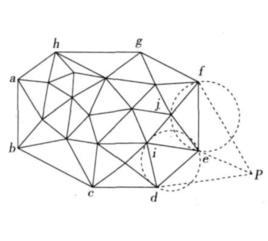
概念
平差值是指用各個小班量算面積之和,與參考面積作差,得出一個數,再用這個數乘以小班所在流域面積的所占百分比得出的數就是這個小班的平差值。
當觀測值含有粗差時,最小二乘平差所具有的優良特性就顯得遜色了。對含有粗差的觀測值進行平差,將使平差結果受到粗差的影響,因此,在平差前應將其剔除。然而,在平差前不一定能夠檢驗和判明。只能將所有的觀測值進行平差,從而提出有粗差嫌疑的觀測值,對這些觀測值逐一進行檢驗,逐一判定是否為粗差,若其中之一是粗差,就將其剔除,剔除一個粗差後進行一次平差值的轉換,根據轉換結果再檢驗、判定和轉換,直至粗差剔除完畢為止。
起算數據誤差對平差值及其精度的影響
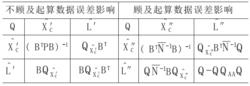 表1 協因數陣表
表1 協因數陣表起算數據誤差對平差值的影響,即為顧及起算數據誤差影響的平差值與不顧及起算數據影響的平差值之差。起算數據誤差對單位權方差的影響仍然是顧及與不顧及起算數據誤差影響的單位權方差之差。
起算數據誤差對平差值協因數陣的影響,也是顧及起始數據誤差影響的平差值協因數陣與不顧及起算數據誤差影響的平差值協因數陣之差。由文獻 知,不顧及起算數據誤差影響和顧及起算數據誤差影響的平差值協因數陣計算公式(間接平差)如表1所示。
起算數據誤差對平差精度的影響
從套用實例可以看出,起始數據對平差值及平差值的精度均有影響。在本例所用觀測高差等權的條件下,影響規律為:對參數平差值的影響的絕對值相等,對各觀測高差平差值影響的絕對值也相等;對平差值協因數的影響均為正值,說明不顧及起算數據誤差影響的平差使平差值協因數變小;對參數平差值方差的影響均為正值,說明不顧及起算數據誤差影響的平差使平差值方差變小,過高地估計了參數平差值的精度;對觀測值平差值方差的影響均為負值,既不顧及起算數據誤差影響的平差使觀測值的方差變大,過低的估計了觀測值平差值的精度。
研究結論
研究給出了分析起算數據誤差影響的方法和計算影響值的共式,並通過對影響值的量化分析,進一步說明了起算數據誤差對例中控制網平差結果的影響規律。對於各類測量控制網,均可按本文給出的方法計算起算數據誤差對網中平差結果的影響,從而分析其影響規律。由於測量控制網是逐級布設的,起算數據誤差對平差結果的累計影響是十分可觀的,是一個必須引起重視和加以研究的問題。
起算數據與待定點平差值精度的關係分析
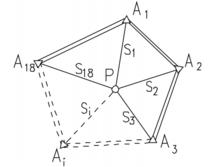 圖1 測邊三角網示意圖
圖1 測邊三角網示意圖在文獻 中,分析了多餘觀測數對精度的影響,並以水準網為例,驗證了隨著起算數據個數的增加,待定點平差值的精度會顯著提高。但是,當多餘觀測數增加到一定程度後,待定點的精度提高並不明顯,或者說精度就不再提高了。因此,以測邊三角網為例,採用間接平差模型,進一步驗證了已知起算數據個數與待定點平差值的精度之間的關係,並得出了有益的結論。
間接平差的原理
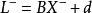 平差值
平差值(1)函式模型:
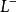 平差值
平差值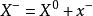 平差值
平差值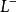 平差值
平差值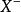 平差值
平差值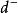 平差值
平差值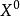 平差值
平差值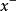 平差值
平差值其中,=L+V,;為觀測值L的平差值,為參數的平差值,為常數項,V為觀測值的改正數,為參數的近似值,為參數的近似值改正數;
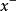 平差值
平差值誤差方程為:V=B-l
(2)實驗算例
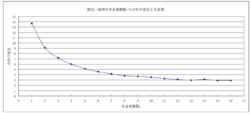 圖2 測邊三角網中多餘觀測數r與中誤差之間的關係曲線圖
圖2 測邊三角網中多餘觀測數r與中誤差之間的關係曲線圖如圖1所示,為一測邊三角網。P為坐標待定的點,A、A、…、A為已知點,S、S、…、S為觀測邊長。
為了求得待定點P的坐標平差值,可以採用A、A兩點和觀測邊長S、S進行計算,也可以採用若干個已知點和更多的觀測邊長來計算。這樣,隨著所使用的已知點個數和觀測邊長個數的增加,所求得的待定點P的坐標平差值的精度也會不斷變化。
觀測數與待定點平差值中誤差關係分析
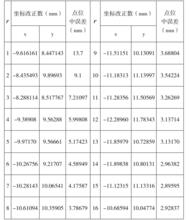 表2 隨著r的變化,測邊三角網依據間接平差計算出的P點數據
表2 隨著r的變化,測邊三角網依據間接平差計算出的P點數據由表2及圖2可以看出,隨著r的增大,點位中誤差總體上逐漸減小。當r≤7時,點位中誤差減小幅度較大;之後隨著r的增大,中誤差減小的幅度越來越小。從理論上,中誤差的取值仍會減小,但在實用上已沒有太大的意義。通過以上的計算可以得出結論,當已知起算數據的個數大於一定數值後,再增加起算數據不會提高待定點的精度。
研究結論
在以上的計算過程中,作者對多餘觀測數與中誤差之間的精度關係進行了分析,但需要注意以下幾個問題:
(1)研究計算中採用間接平差,其參數的近似值只取了一個值。
(2)研究是以測邊三角網為例進行了計算,測邊三角網的函式模型是非線性的,線性化時存在泰勒級數展開項的取捨問題。對於其他網形沒有進行考慮。