區別
雙凸透鏡,兩面入射的光,折射率相同。焦距也一樣。
平凸透鏡,兩面入射的光,折射率稍有差別。所以實際上兩邊的焦距也有所不同。使用時,不能顛倒。
作用
這類透鏡用於匯聚平行光,或把點光源轉化成平行光。
合理選擇材料(紋理,氣泡,雜質,均勻性);在研磨時,考慮到了用於可干涉光時,不產生散亂(劃傷,凹痕,光澤)。
規格品有沒鍍膜和鍍了可見光帶域的防反射多層膜透鏡。
望遠鏡:
1609年5月,著名科學家伽利略45歲的時候訪問了威尼斯。在那裡他聽到了荷蘭人造出望遠鏡的故事,並為此興奮不已。
伽利略馬上動手製造自己的望遠鏡。他在一根鉛管兩端,裝上一片平凸透鏡和一片平凹透鏡。平凹透鏡靠近眼的一端,稱為目鏡。平凸透鏡靠近觀測物一端,稱為物鏡。他用自製的望遠鏡觀測物體時,遠處的物體被放大了許多倍。
伽利略雖然不是第一個發明望遠鏡的人,但以他科學家的敏感,成為第一個將望遠鏡對準星空的人。從此,天文望遠鏡誕生了,天文學獲得了探索宇宙的新武器,並由此取得了一個又一個驚人的發現。
計算舉例
有一定厚度平凸透鏡的焦距公式計算
例如:厚度為5,半徑為20的平凸透鏡的焦距
(1) 如果是凸透鏡平面的圓半徑:
1。計算凸透鏡的球半徑:r^2=20^2+(r-5)^2,r=42.5;
2。做平行於光軸的直線AA',交凸透鏡球面於點A,直線AA"垂直於光軸,與光軸的交點為A",直線段AA"的長度是h,做直線OA、FA,其中O是球心,F是焦點,過點A做凸透鏡球面的切線AB,交光軸於點B,則OA垂直AB,直線OA就是入射光線AA'的法線;
3。計算入射角的正弦值:因為AA'平行光軸OF,因此入射角a=∠AOB,Sin(a)=Sin(AOB)=h/r,∠AOB=ArcSin(h/r);
4。設凸透鏡所用材料的折射率為n,則出射角的正弦值 Sin(b)=Sin(a)/n=(h/r)/n=(h*n)/r,即Sin(OAF)=(h*n)/r,∠OAF=ArcSin[(h*n)/r];
5。∠AFO=∠AOB-∠OAF=ArcSin[(h*n)/r]-ArcSin(h/r),tg(AFO)=tg{ArcSin[(h*n)/r]-ArcSin(h/r)}=AA"/FA"=h/FA",FA"=h/tg{ArcSin[(h*n)/r]-ArcSin(h/r)};
6。一面是平面的薄凸透鏡,光心可以近似的認為是平面的圓心,因此焦距f=OF+(r-5)=(FA"-OA")+(r-5),而OA^2=OA"^2+AA"^2,即OA"=√(OA^2-AA"^2)=√(r^2-h^2);
7。最後,把FA"、OA"代入,化簡計算就可以算出焦距f了。
(2)如果是凸透鏡的球半徑,則以上步驟中的第一步可以省略,直接從第二步開始算起就行了。
曲率半徑
牛頓環儀是由待測平凸透鏡(凸面曲率半徑約為200~700cm)和磨光的平玻璃板疊合裝在金屬框架中構成,當一曲率半徑很大的平凸透鏡的凸面與一磨光平玻璃板相接觸時,在透鏡的凸面與平玻璃板之間將形成一空氣薄膜,離接觸點等距離的地方,厚度相同。若以波長為λ的單色平行光投射到這種裝置上,則由空氣膜上下表面反射的光波將互相干涉,形成的干涉條紋為膜的等厚各點的軌跡,這種干涉是一種等厚干涉。
在反射方向觀察時,將看到一組以接觸點為中心的亮暗相間的圓環形干涉條紋,而且中心是一暗斑,如果在透鏡方向觀察,則看到的干涉環紋與反射光的干涉環紋的光強分布恰成互補,中心是亮斑,原來的亮環處變為暗環,暗環處變為亮環,這種干涉現象最早為牛頓所發現,故稱牛頓環。
原理
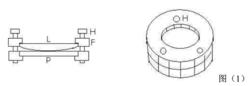 圖1
圖11、 牛頓環
牛頓環儀是由待測平凸透鏡(凸面曲率半徑約為200~700cm)L和磨光的平玻璃板P疊合裝在金屬框架F中構成圖1。框架邊上有三個螺鏇H,用以調節L和P之間的接觸,以改變干涉環紋的形狀和位置。調節H時,螺鏇不可鏇得太緊,以免接觸壓力過大引起透鏡彈性形變,甚至損壞透鏡。
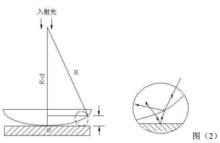 圖2
圖2當一曲率半徑很大的平凸透鏡的凸面與一磨光平玻璃板相接觸時,在透鏡的凸面與平玻璃板之間將形成一空氣薄膜,離接觸點等距離的地方,厚度相同。如圖2所示。若以波長為λ的單色平行光投射到這種裝置上,則由空氣膜上下表面反射的光波將互相干涉,形成的干涉條紋為膜的等厚各點的軌跡,這種干涉是一種等厚干涉。
在反射方向觀察時,將看到一組以接觸點為中心的亮暗相間的圓環形干涉條紋,而且中心是一暗斑(圖3(a))如果在透鏡方向觀察,則看到的干涉環紋與反射光的干涉環紋的光強分布恰成互補,中心是亮斑,原來的亮環處變為暗環,暗環處變為亮環(圖3(b))這種干涉現象最早為牛頓所發現,故稱牛頓環。
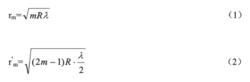 圖一
圖一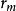 平凸透鏡
平凸透鏡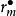 平凸透鏡
平凸透鏡設透鏡L的曲率半徑為R,形成的m級干涉暗條紋的半徑為 ,形成的m級干涉亮條紋的半徑為,不難證明圖一。
以上兩式表明,當λ已知時,只要測出第m級暗環(或亮環)的半徑即可算出透鏡的曲率半徑R,相反,當R已知時,即可算出λ。但由於兩接觸鏡面之間難免附著塵埃,並且在接觸時難免發生彈性形變,因而接觸處不可能是一個幾何點,而是一個圓斑,所以近圓心處環紋比較模糊和粗闊,以致難以確切判定環紋的干涉級數m,即干涉環紋的級數和序數不一定一致。這樣如果只測量一個環紋的半徑,計算結果可能有較大的誤差。為了減少誤差,提高測量精度,必須測量距中心較遠的、比較清晰的兩個環紋的半徑,例如測量出第m1個和第m2個暗環(或亮環)的半徑(這裡m1、 m2均為環序數,不一定是干涉級數),因而圖一(1)式應修正為
 圖3
圖3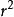 平凸透鏡
平凸透鏡=(m+j)Rλ——————(3)
式中m為環序數,(m+j)為干涉級數(j為干涉修正值),於是如圖3的(4)所示。
上式表面,任意兩環的半徑平方差和干涉級以及環序數無關,而只與兩個環的序數之差(m2-m1)有關。因此,只要精確測定兩個環的半徑,由兩個環的半徑的平方差值就可準確地算出透鏡的曲率半徑R,即圖3的(5)和(6).
補充
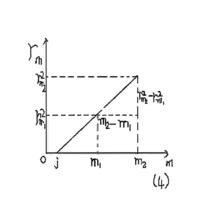 圖4
圖4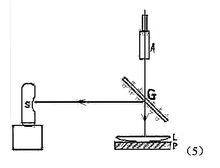 圖5
圖5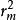 平凸透鏡
平凸透鏡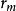 平凸透鏡
平凸透鏡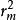 平凸透鏡
平凸透鏡由(3)式可以知道,與m直線關係,如圖4,其斜率為Rλ,因此,也可以測出一組暗環(或亮環)半徑和它們相應的環序數m,作-----m的關係曲線,然後從直線的斜率算出R。

