簡介
在數學裡, 平凡群是指一個只包含單一元素 e的群,其群運算只有 e+ e= e,單位元素平凡是 e,且為阿貝爾群;這些結果都是平凡的,因此以此命名。平凡群通常被寫做 Z,或盡標示為0。
不可把平凡群和空集相混淆,空集中沒有任何元素,因此缺少一個單位元而無法形成一個群,雖然這兩者在其各自的範疇中扮演著極相近的角色。
每一個群都包含著一個平凡群。
阿貝爾群
阿貝爾群(Abelian group)也稱為 交換群(commutative group)或 可交換群,它是滿足其元素的運算不依賴於它們的次序(交換律公理)的群。阿貝爾群推廣了整數集合的加法運算。阿貝爾群以挪威數學家尼爾斯·阿貝爾命名。
阿貝爾群的概念是抽象代數的基本概念之一。其基本研究對象是模和向量空間。阿貝爾群的理論比其他非阿貝爾群簡單。有限阿貝爾群已經被徹底地研究了。無限阿貝爾群理論則是目前正在研究的領域。
阿貝爾群的群運算符合交換律,因此阿貝爾群也被稱為 交換群。它由自身的集合 G和二元運算* 構成。它除了滿足一般的群公理,即運算的結合律、 G有單位元、所有 G的元素都有逆元之外,還滿足交換律公理
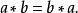 平凡群
平凡群因為阿貝爾群的群運算滿足交換律和結合律,群元素乘積的值與乘法運算時的次序無關。
而群運算不滿足交換律的群被稱為“非阿貝爾群”,或“非交換群”。
性質
如果 n是自然數而 x是使用加號的阿貝爾群 G的一個元素,則 nx可以定義為 x+ x+ ... + x( n個數相加)並且(− n) x= −( nx)。以這種方式, G變成在整數的環 Z上的模。事實上,在 Z上的模都可以被識別為阿貝爾群。
關於阿貝爾群(比如在主理想整環 Z上的模)的定理經常可以推廣到在任意主理想整環上的模。典型的例子是有限生成阿貝爾群的分類是在主理想整環上的有限生成模的結構定理的特殊情況。在有限生成阿貝爾群的情況下,這個定理保證阿貝爾群可以分解為撓群和自由阿貝爾群的直和。前者可以被寫為形如 Z/ p Z對於素數 p的有限多個群的直和,而後者是有限多個 Z的複本的直和。
如果 f, g: G→ H是在阿貝爾群之間的兩個群同態,則它們的和 f+ g,定義為( f+ g)( x) = f( x) + g( x),也是阿貝爾同態。(如果 H是非阿貝爾群則這就不成立。)所有從 G到 H的群同態的集合Hom( G, H)因此是自身方式下的阿貝爾群。
某種程度上類似於向量空間的維度,所有阿貝爾群都有秩。它定義為群的線性無關元素的最大集合的勢。整數集和有理數集和所有的有理數集的子群都有秩1。
另見
•小群列表
