定理
整數帶餘除法定理
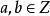 帶餘除法
帶餘除法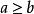 帶餘除法
帶餘除法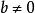 帶餘除法
帶餘除法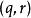 帶餘除法
帶餘除法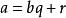 帶餘除法
帶餘除法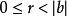 帶餘除法
帶餘除法設,這裡設 ,且 ,存在唯一的整數對 ,使 ,其中 。這個定理稱為整數帶餘除法定理,是初等數論的基礎。
證明:
易得b<0時,與b>0時證明類似,此處為了簡明,僅證明b>0的情況。
【存在性】
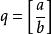 帶餘除法
帶餘除法令 ([x]表示不超過x的最大整數)
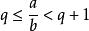 帶餘除法
帶餘除法∵
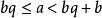 帶餘除法
帶餘除法∴
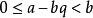 帶餘除法
帶餘除法∴
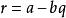 帶餘除法
帶餘除法此時,令
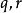 帶餘除法
帶餘除法則 存在,證畢。
【唯一性】
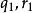 帶餘除法
帶餘除法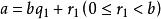 帶餘除法
帶餘除法設 是滿足 的另一對整數,因為
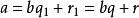 帶餘除法
帶餘除法,
於是
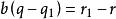 帶餘除法
帶餘除法故
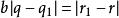 帶餘除法
帶餘除法 帶餘除法
帶餘除法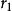 帶餘除法
帶餘除法 帶餘除法
帶餘除法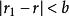 帶餘除法
帶餘除法由於 及 都是小於 的非負整數,所以
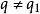 帶餘除法
帶餘除法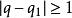 帶餘除法
帶餘除法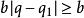 帶餘除法
帶餘除法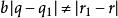 帶餘除法
帶餘除法因為 ,則 , ,故 ,假設不成立
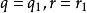 帶餘除法
帶餘除法∴
唯一性證畢
多項式帶餘除法定理
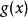 帶餘除法
帶餘除法 帶餘除法
帶餘除法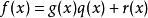 帶餘除法
帶餘除法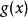 帶餘除法
帶餘除法任意非零多項式 除 ,其商式餘式一定存在,且餘式是惟一滿足關係式 的零多項式,或次數小於 的一個多項式。
多項式除以多項式
多項式除以多項式一般用豎式進行演算
(1)把被除式、除式按某個字母作降冪排列,並把所缺的項用零補齊;
(2)用被除式的第一項除以除式的第一項,得商式的第一項;
(3)用商式的第一項去乘除式,把積寫在被除式下面(同類項對齊),消去相等項,把不相等的項結合起來;
(4)把減得的差當作新的被除式,再按照上面的方法繼續演算,直到餘式為零或餘式的次數低於除式的次數時為止。被除式=除式×商式+餘式。如果一個多項式除以另一個多項式,餘式為零,就說這個多項式能被另一個多項式整除
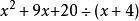 帶餘除法
帶餘除法例如:計算
解:
 帶餘除法
帶餘除法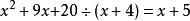 帶餘除法
帶餘除法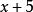 帶餘除法
帶餘除法 帶餘除法
帶餘除法所以,, 其中,商式是,餘式是
套用
輾轉相除法求最大公因式
 帶餘除法
帶餘除法 帶餘除法
帶餘除法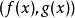 帶餘除法
帶餘除法顧名思義,輾轉相除法就是反覆進行帶餘除法。它以帶餘除法為基礎,是用以求兩個多項式 、 的最大公因式 的一種計算方法。
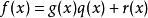 帶餘除法
帶餘除法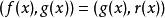 帶餘除法
帶餘除法它的理論依據是:若 ,則有
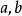 帶餘除法
帶餘除法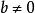 帶餘除法
帶餘除法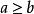 帶餘除法
帶餘除法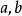 帶餘除法
帶餘除法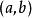 帶餘除法
帶餘除法例如,對於任意的整數 ( ),且 ,求 的最大公約數
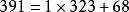 帶餘除法
帶餘除法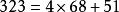 帶餘除法
帶餘除法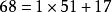 帶餘除法
帶餘除法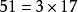 帶餘除法
帶餘除法, , ,
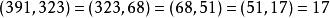 帶餘除法
帶餘除法餘數定理
 帶餘除法
帶餘除法 帶餘除法
帶餘除法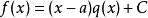 帶餘除法
帶餘除法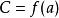 帶餘除法
帶餘除法用一次多項式 去除多項式 ,即 ,其中
 帶餘除法
帶餘除法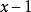 帶餘除法
帶餘除法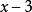 帶餘除法
帶餘除法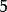 帶餘除法
帶餘除法 帶餘除法
帶餘除法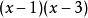 帶餘除法
帶餘除法例:一個多項式 ,當它能被 除時餘式為 3 ,被 除時餘式為 ,則當 被 除時餘式為何?
解:依題意,有:
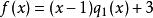 帶餘除法
帶餘除法(1)
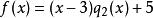 帶餘除法
帶餘除法(2)
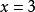 帶餘除法
帶餘除法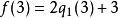 帶餘除法
帶餘除法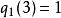 帶餘除法
帶餘除法把 代入(1) 式中, ,得
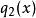 帶餘除法
帶餘除法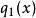 帶餘除法
帶餘除法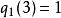 帶餘除法
帶餘除法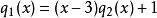 帶餘除法
帶餘除法把餘數定理逆過來用,當用 去除 時,由於 ,有 (3)
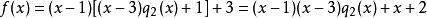 帶餘除法
帶餘除法將(3)代入(1)中,
 帶餘除法
帶餘除法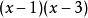 帶餘除法
帶餘除法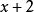 帶餘除法
帶餘除法即 被 除餘式為
整除性問題
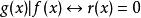 帶餘除法
帶餘除法理論依據 是:
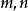 帶餘除法
帶餘除法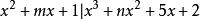 帶餘除法
帶餘除法例:用帶餘除法求當 為何值時,
解:作帶餘除法。
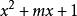 帶餘除法
帶餘除法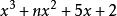 帶餘除法
帶餘除法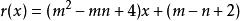 帶餘除法
帶餘除法除 的餘式
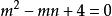 帶餘除法
帶餘除法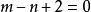 帶餘除法
帶餘除法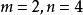 帶餘除法
帶餘除法故 且 ,解得:
