定義
 帕斯卡分布
帕斯卡分布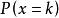 帕斯卡分布
帕斯卡分布在重複、獨立的伯努利試驗,設每次試驗成功的機率為p,失敗的機率為q= 1- p,若將試驗進行到出現r(r為常數)次成功為止,以隨機變數X表示所需試驗次數,則 X是離散型隨機變數,其機率分布為: ,此時稱 服從 帕斯卡分布。其中p表示每次試驗出現成功的機率,而q=1-p,它的期望為r/p,方差為r/(1-p),當r=1時,即為 幾何分布帕斯卡(Pas-cal , B.)。
曾於1654年與費馬(Fermat , P. de)在通信中研討有關機率問題,他們的研究被認為共同奠定了機率論和組合分析的基礎.在他的《算術三角形》一書中,建立了機率論的基本原理和若干重要的組合定理。此分布即由帕斯卡首先引入並載於此書中。
相關公式
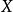 帕斯卡分布
帕斯卡分布 帕斯卡分布
帕斯卡分布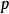 帕斯卡分布
帕斯卡分布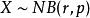 帕斯卡分布
帕斯卡分布若隨機變數 服從參數為 和 的負二項分布,則記為
 帕斯卡分布
帕斯卡分布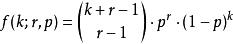 帕斯卡分布
帕斯卡分布當 是整數時,負二項分布又稱 帕斯卡分布,其機率質量函式為 。
 帕斯卡分布
帕斯卡分布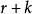 帕斯卡分布
帕斯卡分布 帕斯卡分布
帕斯卡分布它表示,已知一個事件在伯努利試驗中每次的出現機率是 ,在一連串伯努利試驗中,一件事件剛好在第 次試驗出現第 次的機率。
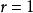 帕斯卡分布
帕斯卡分布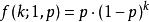 帕斯卡分布
帕斯卡分布取 ,負二項分布等於幾何分布。其機率質量函式為 。
求帕斯卡分布的期望和方差的三種方法 :
方法一:用求離散型隨機變數數學期望的方法來求帕斯卡分布的數學期望和方差;
方法二:利用冪級數的性質求期望和方差;
方法三:將帕斯卡分布分解為若干幾何分布之和。
例子
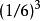 帕斯卡分布
帕斯卡分布舉例說,若我們擲骰子,擲到一即視為成功。則每次擲骰的成功率是1/6。要擲出三次一,所需的擲骰次數屬於集合{ 3, 4, 5, 6, ... }。擲到三次一的擲骰次數是負二項分布的隨機變數。要在第三次擲骰時,擲到第三次一,則之前兩次都要擲到一,其機率為 。注意擲骰是伯努利試驗,之前的結果不影響隨後的結果。
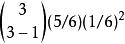 帕斯卡分布
帕斯卡分布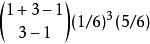 帕斯卡分布
帕斯卡分布若要在第四次擲骰時,擲到第三次一,則之前三次之中要有剛好兩次擲到一,在三次擲骰中擲到2次1的機率為 。第四次擲骰要擲到一,所以要將前面的機率再乘(1/6): 。
套用
某數學家有兩盒火柴,每盒都有n根火柴,每次用火柴時他隨機地在兩盒中任取一盒並從中抽出一根.求該數學家用完一盒時另一盒還有r根火柴的機率 。
這個問題就是歷史上經典的 巴拿赫火柴盒問題,從一盒中取一次火柴視為一次成功試驗,從另一盒中取一次火柴視為一次失敗的試驗,可將問題轉化為 帕斯卡分布。但是根據不同的假設,會有兩個不同的答案。
答案一:
 帕斯卡分布
帕斯卡分布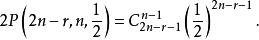 帕斯卡分布
帕斯卡分布不妨設該數學家能夠看到火柴盒裡的火柴且甲盒為空,則他一共在此盒裡取了n次火柴,在乙盒裡取了n- r次火柴,且最後一次取火柴是從甲盒裡取出裡面最後一根.由於數學家取火柴是隨機的,所以從甲盒或乙盒取一次火柴的機率相等,都是12.取火柴問題即為2n- r次重複、獨立的伯努利試驗中有n次成功, n- r次失敗,且最後一次試驗是成功的帕斯卡分布問: ,由甲、乙兩盒的對稱性,得: P{用完一盒時另一盒還有r根火柴}= .
答案二:
 帕斯卡分布
帕斯卡分布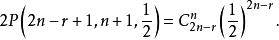 帕斯卡分布
帕斯卡分布不妨設該數學家不能看到火柴盒裡的火柴且甲盒為空,則他一共在此盒裡取了n+ 1次火柴,在乙盒裡取了n- r次火柴,且最後一次取火柴是在已空的甲盒裡又取了一次但發現已空,沒能取到火柴.此問題轉化為2n- r+ 1次重複、獨立的伯努利試驗中有n+ 1次成功,n- r次失敗,且最後一次試驗是成功的帕斯卡分布問題: ,由甲、乙兩盒的對稱性。得:P{用完一盒時另一盒還有r根火柴}=
同一個問題,會產生兩個答案,原因在於對何時火柴盒為空的不同理解上。不論那種答案,都是套用了帕斯卡分布,同時還要考慮兩個火柴盒的對稱性問題。

