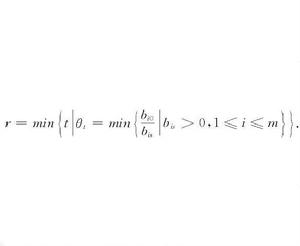基本介紹
布蘭德規則是用單純形法求解線性規劃問題時避免循環的方法。在換基疊代中,選取與下標最小的正檢驗數r相應的非基變數x為入基變數,其中
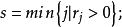 布蘭德規則
布蘭德規則且當出現兩個以上相同的最小比值θ時,選取下標最小的θ相應的基變數 x為出基變數,其中
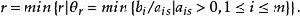 布蘭德規則
布蘭德規則由布蘭德(Robert Gary Bland)於1977年提出。此方法比較簡單,在國際上受到很多人的重視,有利於在計算機上 施行。
相關介紹
單純形法(simplex method)是求解線性規劃問題的基本方法,此方法是丹齊克(G.B.Dantzig)於1947年提出來的.方法的基本思路是:根據線性規劃問題的標準型形式,從可行域中一個基可行解開始,變換到另一個基可行解,並且使目標函式的值逐步增大;當目標函式達到最大值時,就得到了該線性規劃問題的最優解,由於線性規劃問題僅有有限個基可行解,所以如不出現循環,全部疊代過程可在有限次內終止.此時,或者已得到問題的最優解,或者判定問題無有限最優解 。
換基疊代(basis iteration)一般是指求解線性規劃問題過程中的疊代技巧,是從一個基可行解到另一個基可行解的疊代。在單純形表上的換基疊代過程是:
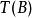 布蘭德規則
布蘭德規則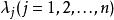 布蘭德規則
布蘭德規則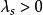 布蘭德規則
布蘭德規則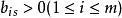 布蘭德規則
布蘭德規則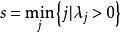 布蘭德規則
布蘭德規則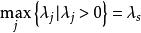 布蘭德規則
布蘭德規則1.確定入基變數。若在 的檢驗數 中有檢驗數 ,且λ所在列的其他元素中有 ,則取 ,即T(B)中最左邊的一個正檢驗數λ(或取 ),讓其對應的變數x為入基變數。
2.求主元,確定出基變數。按最小比值原則
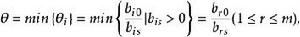 布蘭德規則
布蘭德規則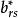 布蘭德規則
布蘭德規則其中b為主元,記為 ,主元b所在行的基變數x就是要確定的出基變數。
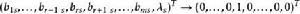 布蘭德規則
布蘭德規則3.以b為主元,進行初等行變換。將入基變數x所在的列變為單位向量,即 ,與此同時,原T(B)中的各元素按以下各式計算,變為相應的新元素:
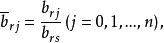 布蘭德規則
布蘭德規則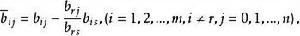 布蘭德規則
布蘭德規則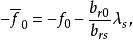 布蘭德規則
布蘭德規則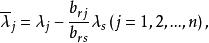 布蘭德規則
布蘭德規則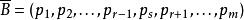 布蘭德規則
布蘭德規則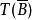 布蘭德規則
布蘭德規則於是得到新基 所對應的單純形表 。