概念解釋
是相對差異量數中的一種測度,又名“變異係數”,通常以CV代表之。在統計中,兩極差、四分位差、平均差和標準差都屬於絕對差異量數。這種差異量數具有與原始資料相同的單位,可用以比較兩種差異量的大小。但遇到兩種資料的單位不同,或資料的單位雖然相同,但平均數相差甚大時,仍用絕對差異量進行比較,其所得結果則往往不可靠。在這種情況下,則必須使用差異係數。差異係數由於是相對差異量數,它既可用於不同單位資料的差異比較,也可用於不同水平的同類現象的差異情況的比較。
最常用的差異係數是由皮爾遜(Pearson,K.)所提出的。所謂差異係數就是以平均數去除標準差再乘以100%,化成百分比的形式。其計算公式為:
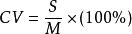 差異係數
差異係數式中S為標準差,M為平均數。
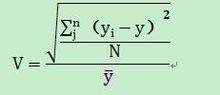 差異係數
差異係數差異係數通常用標準差計算,因此,差異係數也被稱為標準差係數。其計算公式為:
離散係數大,代表其數據的離散程度大,其平均數的代表性就差,反之亦然。
常用比較
常用於兩個方面相對差異量的比較。一是不同質的測量,例如身高與體重各自變異大小的比較,不能直接用標準差,因為二者測量單位不同,而應根據各自的平均數與標準差計算變異係數後再比較。二是測量單位相同、但不同樣本的數據相差較大,在這種情況下,一般平均數較大的樣本標準差也較大,平均數較小的樣本標準差也較小,不能直接用標準差比較變異大小。例如兒童的身高和成人的身高雖然都用長度單位表示,但兩樣本平均數相差較大,標準差相差也大。欲比較相對差異,都須轉換成變異係數。不過相對差異量的比較至今沒有檢驗的方法,只依數值大小作簡單的算術比較。變異係數值大則變異程度大,反之則小。

