左矢量

在量子力學中，所有的物理規律在一個希爾伯特空間中表示，而這個希爾伯特空間（可以簡易地先理解為無限維酉空間）中的一個矢量代表一個可能的物理態，這個矢量空間是右矢量空間；左矢量空間定義為右矢量空間的對偶（dual ）空間。每一個右矢量都有一個左矢量與之對偶。

名稱

其英文名的起源是將單詞braket分成了兩部分，bra表示左矢量，ket表示右矢量。

表示

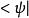左矢量

一般而言，在量子力學中一個右矢量我們會採取如下記號 ：

在不同表象（representation ）下，同一左矢量的表示也會不同，比如動量為p的平面波，我們標記其左矢量為<p|：

其在動量表象下的表示：

左矢量

<p|p'>= (p'-p)

其在坐標表象下的表示卻為：

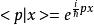左矢量

性質

作為右矢量空間的對偶空間，左矢量空間也是希爾伯特空間，故而具有線性 。

左矢量空間和右矢量空間在一起定義了內積運算，即：

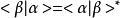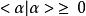左矢量

左矢量

這樣其構成一個酉空間。

值得注意的是，對於線性中的數乘而言，將不改變右矢量所代表的物理態，而考慮到幾率振幅的歸一化，一般我們都會選取歸一的右矢量，而其所對偶的左矢量也是歸一的：

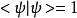左矢量

我們認為算符作用在右矢量上相當於對其進行一次線性變換，類似地，我們也可以認為算符共軛地作用在左矢量上，即若：

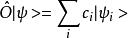左矢量

則有：

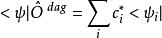左矢量