概念
取左矢量(或右矢量)的一個集合,使任意左矢量(或右矢量)都能表示為它們的線性組合。這些左矢量(或右矢量)稱為表象的基左矢(或基右矢)。基左矢和基右矢總稱為基矢量。
在量子力學中,總是選一組完整的力學量的本徵函式系所對應的左矢量(或右矢量)來作為基矢量。
基本原理
協變基矢量
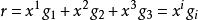 基矢量
基矢量 由式求矢徑對坐標的微分:
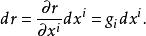 基矢量
基矢量 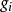 基矢量
基矢量 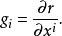 基矢量
基矢量 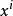 基矢量
基矢量 將矢徑對坐標的偏導數定義為協變基矢量,稱為自然基矢量。即協變基矢量的方向沿坐標線正方向,其大小等於當坐標有1單位增量時兩點之間的距離。因三個坐標線非共面,故
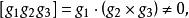 基矢量
基矢量 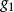 基矢量
基矢量 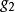 基矢量
基矢量 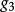 基矢量
基矢量 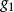 基矢量
基矢量 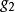 基矢量
基矢量 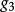 基矢量
基矢量 即,,線性無關。當,,構成左手系時,混合積為正值,記
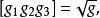 基矢量
基矢量 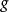 基矢量
基矢量 式中是一個正實數。
逆變基矢量
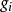 基矢量
基矢量 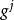 基矢量
基矢量 定義一組3個與協變基矢量互為對偶的逆變基矢量,滿足對偶條件:
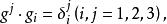 基矢量
基矢量 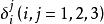 基矢量
基矢量 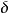 基矢量
基矢量 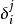 基矢量
基矢量 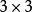 基矢量
基矢量 式中為三維的克羅內克爾,構成的單位矩陣。
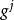 基矢量
基矢量 逆變基矢量與協變基矢量的關係見圖1示,
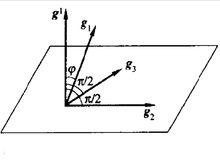 圖1
圖1 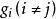 基矢量
基矢量 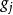 基矢量
基矢量 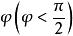 基矢量
基矢量 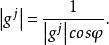 基矢量
基矢量 其方面垂直於另兩個協定基矢量,並與有夾角,其模為
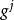 基矢量
基矢量  基矢量
基矢量 今後可以證明,逆變基矢量實際上是垂直於坐標的等值面(即坐標面)的梯度。

