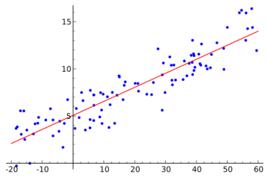
簡介
嶺回歸，又稱脊回歸、吉洪諾夫正則化（Tikhonov regularization），是對不適定問題（ill-posed problem)進行回歸分析時最經常使用的一種正則化方法。
原理
對於有些矩陣，矩陣中某個元素的一個很小的變動，會引起最後計算結果誤差很大，這種矩陣稱為“病態矩陣”。有些時候不正確的計算方法也會使一個正常的矩陣在運算中表現出病態。對於高斯消去法來說，如果主元（即對角線上的元素）上的元素很小，在計算時就會表現出病態的特徵。
回歸分析中常用的最小二乘法是一種無偏估計。對於一個適定問題，X通常是列滿秩的
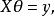嶺回歸採用最小二乘法，定義損失函式為殘差的平方，最小化損失函式
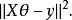嶺回歸上述最佳化問題可以採用梯度下降法進行求解，也可以採用如下公式進行直接求解
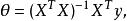嶺回歸
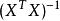嶺回歸 嶺回歸
嶺回歸當X不是列滿秩時，或者某些列之間的線性相關性比較大時， 的行列式接近於0，即 接近於奇異，上述問題變為一個不適定問題，此時，計算 時誤差會很大，傳統的最小二乘法缺乏穩定性與可靠性。
為了解決上述問題，我們需要將不適定問題轉化為適定問題：我們為上述損失函式加上一個正則化項，變為
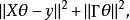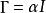嶺回歸
嶺回歸其中，我們定義，於是：
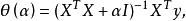嶺回歸
嶺回歸上式中， 是單位矩陣。
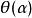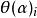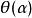嶺回歸
嶺回歸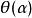
嶺回歸
嶺回歸 嶺回歸 嶺回歸 嶺回歸 嶺回歸 嶺回歸 嶺回歸隨著 的增大， 各元素 的絕對值均趨於不斷變小，它們相對於正確值 的偏差也越來越大。 趨於無窮大時， 趨於0。其中， 隨 的改變而變化的軌跡，就稱為嶺跡。實際計算中可選非常多的 值，做出一個嶺跡圖，看看這個圖在取哪個值的時候變穩定了，那就確定 值了。
嶺回歸是對最小二乘回歸的一種補充，它損失了無偏性，來換取高的數值穩定性，從而得到較高的計算精度。
特點
通常嶺回歸方程的R平方值會稍低於普通回歸分析，但回歸係數的顯著性往往明顯高於普通回歸，在存在共線性問題和病態數據偏多的研究中有較大的實用價值。
