定義
連通空間
定義1：設X是一個拓撲空間。如果X中有兩個非空的隔離子集A和B，使得X= A∪ B，則稱X是一個不連通空間；否則，則稱X是一個連通空間。
局部連通空間
定義2：設X是一個拓撲空間。如果x∈ X的每一個鄰域中都包含著x的某一個連通的鄰域V，則稱拓撲空間在點x處是局部連通的。如果拓撲空間X在它的每一個點處都是局部連通的，則稱是一個局部連通空間 。
局部連通空間局部連通的拓撲空間也不必是連通的。例如，每一個離散空間都是局部連通空間，但包含著多於一個點的離散空間卻不是連通空間。又例如，n維歐氏空間的任何一個開子空間都是局部連通的(這是因為每一個球形鄰域都同胚於整個歐氏空間，因而是連通的)，特別地，歐氏空間本身是局部連通的。另一方面，歐氏空間中由兩個無交的非空開集的並作為子空間就一定不是連通的。
局部連通空間此外根據定義立即可見：拓撲空間X在點xX處是局部連通的若且唯若x的所有連通鄰域構成點二處的一個鄰域基。
道路連通空間
定義3：設X是一個拓撲空間，如果對於任何x, y，存在著X中的一條從x到y的道路(或曲線)，我們則稱X是一個道路連通空間。X中的一個子集Y稱為X中的一個道路連通子集，如果它作為X的子空間是一個道路連通空間。
局部連通空間
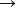局部連通空間 局部連通空間實數空間R是道路連通的，這是因為如果x, yR，則連續映射f： [0,1]R定義為對於任何t[0,1]有f(t)=x+t(y-x)，便是R中的一條以x為起點以y為終點的道路。也容易驗證任何一個區間都是道路連通的 。
與連通空間
（1）定理1：拓撲空間的兩個不同的連通分支是不相交的。
局部連通空間證明：設A和B是兩個連通分支，且A∩ B≠，則由熊金誠的結果 可知，A∪ B是連通的，於是，A= A∪ B=B。
（2）定理2：任何拓撲空間都等於它的連通分支的並集。
證明：在拓撲空間X中，對於任意x∈ X，包含x的連通分支Cx是存在的，所以：
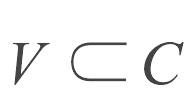局部連通空間（3）定理3：拓撲空間為局部連通的充分必要條件是每一開集的每一連通分支是開集。
證明：設X是局部連通空間，U是X的一個開集，而C是U的一個連通分支。如果x∈ C，由於U是x的一個鄰域，所以x有一個連通鄰域V包含於U。又由於V∩ C包含著點x，所以不是空集。根據熊金程的《點集拓撲講義》 中的定理4.31，可見：
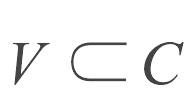局部連通空間因此C是點x的一個鄰域。這證明C是屬於它的任何一個點x的鄰域，因此C是開集。反過來，如果每一個開集的連通分支都是開集，則每一點的每一開鄰域都包含連通的開鄰域，這就是此開鄰域的連通區。因此空間是局部連通的連通空間不一定是局部連通的空間 。
道路連通空間
局部連通空間不一定是道路連通的。
反例：實直線R上的點集E=(- 1,0)∪(0,1)，並把E看成是R上的子空間，則E是局部連通的，但不是連通的。因為0點不屬於E。
