簡化Nyquist穩定判據的描述
由於對於一個穩定的閉環系統來說，其在S右半平面肯定是無特徵根，即Z=0，因此，Nyquist穩定判據就可以這樣認為，若Nyquist曲線包圈(-1，j0)點的圈數等於開環傳函在S右半平面的極點數，則閉環系統穩定。進而，若開環傳函在S右半平面無極點，即P0，則閉環就穩定的充分必要條件是Nyquist曲線不包圍(-1，j0)點。
Nyquist曲線的簡介
對於w的複變函數G(jw)有：
尼奎斯特曲線
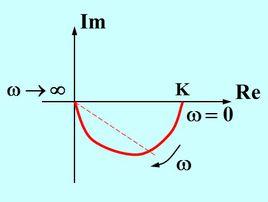
尼奎斯特曲線當ω從0→ 變化時，矢量G(jw)的端點在複平面上形成的軌跡叫作G(jω)的極坐標圖或Nyquist圖，該軌跡就是Nyquist曲線。
Nyquist圖的優點是：在概念分析上比較清楚、直觀，特別在分析系統穩定性上經常用到。Nyquist圖的缺點點是：極坐標圖畫起來複雜，運算也較繁瑣，要遵循矢量運算規則。
Nyquist曲線繪製步驟
Nyquist曲線繪製的大致步驟如下：
（1）寫出系統開環傳遞函式的頻率特性；
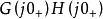尼奎斯特曲線（2）確定開環幅相曲線的起點 ；
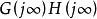尼奎斯特曲線（3）確定開環幅相曲線的終點 ；
（4）確定開環幅相曲線與實軸是否有交點，若有，則該點的頻率特性虛部為零；
（5）確定開環幅相曲線與虛軸是否有交點，若有，則該點的頻率特性實部為零；
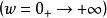尼奎斯特曲線（6）勾畫出開環幅相曲線 的大致曲線(越精確越好)。
Nyquist曲線繪製的注意事項
尼奎斯特曲線
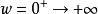尼奎斯特曲線
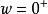尼奎斯特曲線
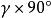尼奎斯特曲線
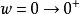尼奎斯特曲線(1) 若系統開環傳遞函式中出現積分環節，說明系統中有零極點，則應對Nyguist曲線進行修正後，才能使用Nyguist穩定判據進行判斷。若開環傳遞函式中有個積分環節，則先繪出的Nyguist曲線，然後從開始，逆時針方向補畫一個半徑為無窮大，相角為的大圓弧，即補畫的曲線，然後再根據Nyguist穩定判據判斷閉環系統的穩定性。
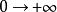尼奎斯特曲線(2) G(jw)與G(-jw)關於實軸對稱，因此只需要w從的Nyguist曲線即可。
(3) 若存在多個環節，應注意隨著w的增加、角度的變化過程以決定Nyguist曲線的變化趨勢。
(4) 判據中的S的右半平面指的是開右半平面，不包括虛軸。
(5) 若Nyguist圖正好通過(-1，j0)點，則閉環系統存在虛軸上的極點，計算N時不視為一次包圍。如果求得Z=0，則閉環系統臨界穩定。
(6) Nyquist圖會同時存在既有逆時針包圍又有順時針包圍(-1，j0)點的情況。N>0表示逆時針包圍(-1，j0)點N圈，N<0表示順時針包圍(-1，j0)點N圈。
Nyquist曲線的穿越問題
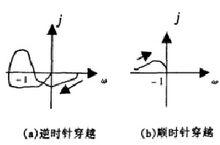圖1 整次穿越圖根據不同的開環傳函Nyquist圖會同時存在既有逆時針包圍又有順時針包圍(-1，j0)點的情況。而Nyquist穩定判據中所提到的“逆時針包圍(-1，j0)點的圈數”是指逆時針包圍和順時針包圍圈數的代數和，即存在逆時針穿越和順時針穿越。
逆時針穿越：隨著w的增大，Nyquist圖逆時針穿越(-1，j0)點左側的負實軸，稱為逆時針穿越，如圖1(a)所示。
圖2 半次穿越圖順時針穿越：隨著w的增大，Nyquist圖順時針穿越(-1，j0)點左側的負實Niquist圖包圍(-1，j0)點的圈數，是S平面上1+Q(s)包圍原點圈數的一半(Q(s)為系統開環傳遞函式，因此，1+Q(s)包圍原點的圈數為奇數時，Nyquist圖將會產生半次包圍(-1，j0)點的情況，會產生“半次穿越”，半次穿越記為1/2。
逆時針半次穿越：Nyquist圖起始於(或終止於)(-1，j0)點左側的負實軸，若沿逆時針方向離開負實軸，稱為逆時針半次穿越。如圖2(a)所示。
順時針半次穿越：Nyquist圖起始於(或終止於)(-1，j0)點左側的負實軸，若沿順時針方向離開負實軸，稱為順時針半次穿越，如圖2(b)所示。
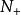尼奎斯特曲線
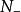尼奎斯特曲線
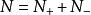尼奎斯特曲線用表示逆時針穿越和逆時針半次穿越次數之和，用表示順時針穿越和順時針半次穿越次數之和，則Nyquist穩定判據中的N可表示為。
