對稱的關係
亦你“具有對稱性的關係”。對於類k中一個確定的關係R來說,類k中的任意兩個個體x,y, 如果xRy真yRx就必真,則稱關係R為類k中 對稱的關係(對稱關係), 如果xRy真yRx就必假, 則稱關係R為類K中 反對稱的關係(反對稱關係);如果對於某些個體x,y, xRy真同時yRx也真, 而對於另外的個體x,y,xRy真時yRx卻假,則稱關係R為類k中 非對稱的關係(非對稱關係)。例如,兩條直線之間的平行關係、垂直關係、 兩個數之間的相等關係等都是 對稱的關係;兩個實數之間的大於關係、 小於關係等部是 反對稱的關係,兩個實數之間的不大於關係, 不小於關係等則是 非對稱的關係, 這是因為由a不大於b, 並不能斷定b是否不大於a。
對稱性關係推理
對稱性關係推理是指前提和結論都是具有對稱性的關係判斷的推理。 所謂對稱性關係是指:當,且僅當對象a和b之間有一定關係時, 對象b和a之間也有這種關係。如,等於關係、某些親屬關係、同一關係、 同時關係,同地關係,全異關係等都屬於 對稱性關係。 根據這些對稱性關係進行推演的關係推理都是 對稱性關係推理。例如,數學裡的“a=b, 所以,b=a,”就屬於具有 等於性的對稱性關係推理。如,“a是b的兄弟,所以,b也是a的兄弟。”這就是表示 某些親屬關係的對稱性的關係推理。 又如,“李白和杜甫是同時代的人,所以, 杜甫和李白是同時代的人。”這是表示 同時關係的對稱性關係推理。
對稱性關係推理可以用如下的公式來表示:R(a,b)→R(b,a)。或者是:aRb,所以, bRa。在這裡,R代表對稱性關係,a和b分別為兩類對象。 對稱性關係推理的規則:如果判斷R(a,b)真,那么,R(b,a)也真。
關係判斷
關係判斷的定義
關係判斷是斷定對象與對象之間關係的簡單判斷。簡單判斷除了性質判斷以外,還有關係判斷,關係判斷是斷定對象與對象之間關係的判斷。
例如:①長江長於黃河;②鄭州在洛陽與開封之間;③笑比哭好;④徐特立與毛澤東有師生關係。這四個判斷都是關係判斷。例①斷定了“長江”與“黃河”之間有“長於”的關係;例②斷定了“鄭州”和“洛陽”、“開封”三者之間存在前者在後面二者之間的“在...之間”的關係;例③斷定了“笑”與“哭”之間有“比....好”的關係;例④判定了“徐特立”與“毛澤東”之間有“師生關係”。
關係判斷和性質判斷不同。性質判斷是斷定對象是否具有某種性質(即對象與性質之間的關係) 的判斷,主項只有一個; 而關係判斷卻是斷定對象與對象之間是否具有某種關係的判斷,而關係總是存在於兩個或兩個以上的對象之間,因此,關係判斷的對象就有兩個或兩個以上,即主項至少是兩個。存在於兩個對象之間的關係叫 兩項關係,存在於三個對象之間的關係叫 三項關係,存在於三個以上對象之間的關係叫 多項關係 。
關係判斷的組成
關係判斷由三部分組成: 關係者項、 關係項、 量項。
關係者項。反映一定關係承擔者的概念(或表示一定關係所聯結的概念),也就是關係判斷的主項。如前述各例中的“長江"、“黃河’,、“鄭州"、“開封"、“笑’’、“哭"、“徐特立"、“毛澤東’’。在關係判斷中,關係者項至少有兩個,也可以是三個或多個。在兩項關係中,在前的關係者項叫關係者前項,在後的關係者項叫 關係者後項。若有三個以上關係者項,則按先後次序可分別稱之為第一、第二、第三……關係者項。 通常用“a"、“b’’、 “c”……表示。
關係項。表示各關係者項之間的關係的概念,也就是關係判斷的謂項。上述各例中的“長於"、“比……好”、“師生關係"、“在……之間”都是關係項, 通常用“R"表示。
量項(關係量項)。表示關係者項數量的概念。每一個關係者項都可以有量項。如“有的美國人高於所有中國入"。其中,“有的”“所有"都是關係者項的量項 。
關係判斷的結構式
根據上述關係判斷的組成要素,我們就可以把具有兩項關係的判斷的結構式表示為;所有(有的)aR有的(所有)b。具體表達為四種基本形式。
所有aR所有b;
所有aR有的b;
有的aR所有b;
有的aR有的b。
實際上,關係判斷既有肯定形式,又有否定形式。例如“5大於3"是肯定關係判斷。而“3不大於5”,就是否定關係判斷。它否定了“3”對於“5’’具有“大於"的關係。這樣,兩項關係判斷的基本形式應該還有另外幾種。
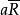 對稱關係
對稱關係所有 所有b;
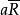 對稱關係
對稱關係所有 有的b;
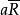 對稱關係
對稱關係有的 有的b;
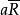 對稱關係
對稱關係有的 所有b。
在關係判斷中,如果關係者項表示的是一個或一類對象,量項可以省略。這樣,二項關係判斷可以寫為:
R(a、b)或aRb;
一個三項的關係判斷可寫為:
R(a、b,c);
關係的分類
對象間的關係多種多樣,因而關係判斷中的關係也有多種多樣。關係判斷的邏輯性質取決子關係的性質。常見的有兩種性質的關係: 對稱性關係(對稱關係、反對稱關係、非對稱關係); 傳遞性關係(傳遞關係;反傳遞關係;非傳遞關係)。

