簡介
對偶圖形(dual figures)，具有特定關係的兩個圖形。指成對偶對應的幾何圖形。射影幾何中一個圖形與把其中的各個幾何元素換成對偶元素，把其中的各個運算換成對偶運算而得到的另一個圖形間的關係。
例如，在射影平面上，把由點和直線所組成的一個圖形中的各元素改為它的對偶元素，各運算改為它的對偶運算，其結果形成另一個圖形，這兩個圖形稱為對偶圖形。又如在三維射影空間中，把由點、直線和平面所組成的一個圖形中各元素改為它的對偶元素，各運算改為它的對偶運算，其結果形成另一個圖形，這兩個圖形稱為空間中的對偶圖形。
其中對偶元素是射影幾何的一個數學術語，指射影幾何中元素間的一種特殊關係。在射影平面上，點與直線互為對偶元素。在三維射影空間中，點與平面互為對偶元素，直線的對偶元素仍是直線。
相關定義
定義1，“點”與“直線”叫做射影平面上的對偶元素。
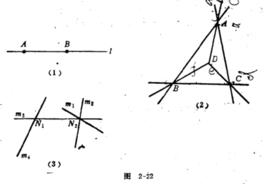
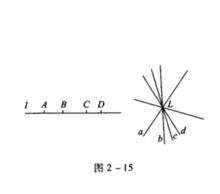圖1定義2，“過一點作一直線”與“在一直線上取一點”叫做對偶作圖。
定義3，設有點和直線做組成的圖形，將此圖形中各元素改為它的對偶元素，各作圖改為對偶作圖，其結果形成另一圖形，這兩個圖形叫做對偶圖形。
由此定義可知，點列和線束是對偶圖形，如右圖1所示。
屬於同一平面的所有點的集合叫點場（點域），所在平面叫點場的底。點場的對偶圖形是屬於同一平面的所有直線的集合，叫做線場（線域），所在平面叫做線場的底。
點列和線束叫做一維基本形。點場與線場叫做二維基本形。
舉例
作出下列圖形的對偶圖形。
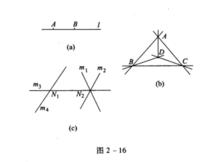
對偶圖形其對偶圖形如下圖所示。
對偶圖形作為對偶圖形的例子，我們引進後面常用的一些簡單平面圖形及其對偶圖形。
簡單四點形
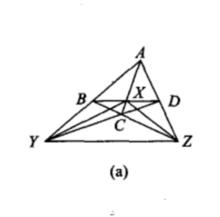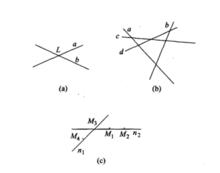
對偶圖形由四個點（其中無三點共線）以及連結其中任意兩點的六條直線所組成的圖像叫完全四點形（右圖a）。這四個點叫定點，六條直線叫邊，沒有公共頂點的兩邊叫對邊，共有三對對邊，三對對邊的交點叫對邊點，它們構成一個三點形，叫對邊三點形。
簡單四線形
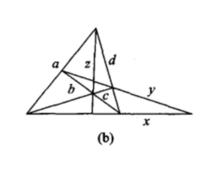對偶圖形由四條直線（其中無三線共點）以及其中任意兩條直線的六個交點所組成的圖形叫完全四邊形（右圖b）。這四條直線叫邊，六個點叫頂點，不在公共邊上的兩頂點叫對頂，共有三對對頂，三對對頂的連線叫對頂線，它們構成一個三線形，叫對頂三線形。
