基本概念
 配極圖形
配極圖形 配極圖形
配極圖形 配極圖形
配極圖形 配極圖形
配極圖形 配極圖形
配極圖形 配極圖形
配極圖形 配極圖形
配極圖形 配極圖形
配極圖形 配極圖形
配極圖形 配極圖形
配極圖形給定二次曲線,如果對平面上的每個點P,使P對應於點P關於的極線,又對平面上的每條直線,使對應於直線關於的極點,則在平面上的點與直線之間就建立了一個一一對應。這個對應稱為關於的 配極或 配極變換。在給定空間二次曲面的情況下,同樣可以通過使點對應於它的極面和使平面對應於它的極點來定義關於的配極或配極變換。配極變換是一種對偶變換。
某個圖形在關於一條二次曲線的配極變換下的象,稱為原來圖形的 配極圖形。給定的二次曲線在關於它本身的配極變換下的象,就成為二級曲線。二級曲線是二次曲線的配極圖形。也可以類似地考慮關於二次曲面的配極圖形 。
配極對應與配極圖形
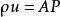 配極圖形
配極圖形在射影平而上,給定一非退化二階曲線,其極點與極線構成了點與直線之間的一一對應關係。該同底點列與線束之間的對應稱為 配極對應,配極對應是一種異素對應,其代數表達式為,即
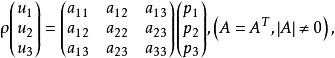 配極圖形
配極圖形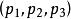 配極圖形
配極圖形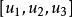 配極圖形
配極圖形其中與是對應極點與極線的坐標 。
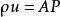 配極圖形
配極圖形在配極對應下,射影平面上任一由點和直線構成的圖形F對應於一由直線和點構成的圖形F',F、F'稱為一對相互配極的圖形。當一個圖形的配極圖形與自身重合時稱之為自配極的,自極三點形就是一個自配極的圖形。
配極對應是非奇異的線性對應。於是,共線四點的交比與其四條對應極線(共點四線)的交比相等。
射影平面上一般的點線異素對應的代數表達式為
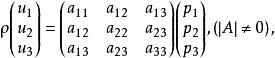 配極圖形
配極圖形這裡不要求A=A ,也是非奇異的線性對應 。
關於球的配極圖形
下面是極線最重要的性質。
定理 若點a在點b的極線上,那么反過來,點b也在點a的極線上 。
此時兩點a和b稱為對於圓的共軛點。它們的極線,就是說一條通過另外一條的極的兩直線,也就稱為共軛直線。
由於點a在點b的極線上(圖1),那么它在Ob上的射影是一點K,滿足Ok ·Ob=R ,設H是b在Oa上的射影;四邊形aHbK可內接於一圓周(以線段ab做直徑的圓周),因而有
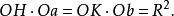 配極圖形
配極圖形所以直線Hb是點a的極線。
備註:若直線ab與圓相交,定理是顯然的。因為,此時假設和結論表達同一回事:圓周調和分割ab。
上面的定理,使我們可以從一個圖形(F)的性質,得到另一個圖形(F')的性質,我們立刻來定義這圖形(F’),它稱為(F)的 配極圖形或 異素射(影)變(換)形 。
設(F)是由若干點和直線組成的圖形(配極圖形的定義也可以推廣於含曲線的圖形),此形的每一點a我們使它對應於一直線A,即點a對於某一圓的極線,這圓稱之為導圓,一經選定便再也不變,圖形(F)的每一直線B使之對應於一點b,即此直線對於導圓的極。直線A和點b組成一個圖形(F’),即(F)的配極形。
由上面的定理得出以下的命題:
若圖形(F)的直線B通過點a,那么圖形(F')的對應點b在點a的對應線A上。
因此,若圖形(F)的一直線繞一定點旋轉,那么圖形(F')的對應點描畫一直線,反之亦然。
或者說,若圖形(F)的三線共點,則圖形(F')的對應三點共線,反之亦然 。

