簡介
富里埃變換將函式的時域(紅色)與頻域(藍色)相關聯。頻譜中的不同成分頻率在頻域中以峰值形式表示。傅立葉變換源自對富里埃級數的研究。在對富里埃級數的研究中,複雜的周期函式可以用一系列簡單的正弦、餘弦波之和表示。富里埃變換是對富里埃級數的擴展,由它表示的函式的周期趨近於無窮。
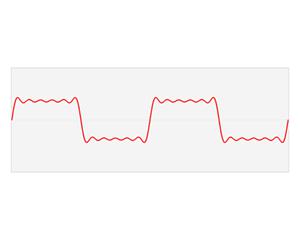 圖1.福里埃變換
圖1.福里埃變換富里埃變換在數據科學、物理學、聲學、光學、結構動力學、量子力學、數論、組合數學、機率論、統計學、訊號處理、密碼學、海洋學、通訊、金融等領域都有著廣泛的套用。例如在訊號處理中,富里埃變換的典型用途是將訊號分解成振幅分量和頻率分量。
定義
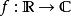 富里埃變換
富里埃變換一般情況下,若“富里埃變換”一詞不加任何限定語,則指的是“連續富里埃變換”(連續函式的富里埃變換)。定義富里埃變換有許多不同的方式。本文中採用如下的定義:(連續)富里埃變換將可積函式 表示成復指數函式的積分或級數形式。
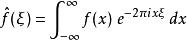 富里埃變換
富里埃變換,ξ為任意實數。
 富里埃變換
富里埃變換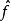 富里埃變換
富里埃變換 富里埃變換
富里埃變換自變數 表示時間(以秒為單位),變換變數ξ表示頻率(以赫茲為單位)。在適當條件下, 可由 逆變換(inverse Fourier transform)由下式確定 :
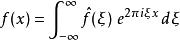 富里埃變換
富里埃變換,x為任意實數。
 富里埃變換
富里埃變換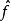 富里埃變換
富里埃變換 富里埃變換
富里埃變換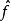 富里埃變換
富里埃變換富里埃逆定理提出 可由 確定,傅立葉在其1822年出版的著作《熱分析理論》中首次引入這個定理。雖然現在標準下的證明直到很久以後才出現。 和 常常被稱為傅立葉積分對或傅立葉變換對。
基本性質
線性性質
 富里埃變換
富里埃變換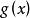 富里埃變換
富里埃變換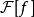 富里埃變換
富里埃變換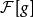 富里埃變換
富里埃變換 富里埃變換
富里埃變換 富里埃變換
富里埃變換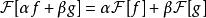 富里埃變換
富里埃變換 富里埃變換
富里埃變換兩函式之和的富里埃變換等於各自變換之和。數學描述是:若函式 和 的富里埃變換 和 都存在, 和 為任意常係數,則 ;富里埃變換算符 可經歸一化成為么正算符。
平移性質
 富里埃變換
富里埃變換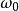 富里埃變換
富里埃變換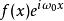 富里埃變換
富里埃變換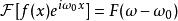 富里埃變換
富里埃變換 富里埃變換
富里埃變換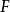 富里埃變換
富里埃變換 富里埃變換
富里埃變換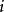 富里埃變換
富里埃變換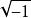 富里埃變換
富里埃變換若函式 存在富里埃變換,則對任意實數 ,函式 也存在富里埃變換,且有 。式中花體 是富里埃變換的作用運算元,平體 表示變換的結果(複函數), 為自然對數的底, 為虛數單位 。
微分關係
 富里埃變換
富里埃變換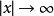 富里埃變換
富里埃變換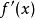 富里埃變換
富里埃變換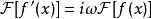 富里埃變換
富里埃變換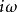 富里埃變換
富里埃變換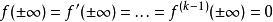 富里埃變換
富里埃變換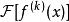 富里埃變換
富里埃變換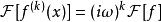 富里埃變換
富里埃變換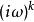 富里埃變換
富里埃變換若函式 當 時的極限為0,而其導函式 的富里埃變換存在,則有 ,即導函式的富里埃變換等於原函式的富里埃變換乘以因子 。若 ,且 存在,則 ,即k階導數的富里埃變換等於原函式的富里埃變換乘以因子 。
卷積特性
 富里埃變換
富里埃變換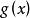 富里埃變換
富里埃變換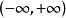 富里埃變換
富里埃變換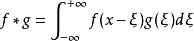 富里埃變換
富里埃變換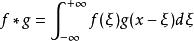 富里埃變換
富里埃變換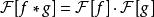 富里埃變換
富里埃變換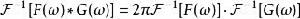 富里埃變換
富里埃變換 富里埃變換
富里埃變換若函式 及 都在 上絕對可積,則卷積函式 (或者 )的富里埃變換存在,且 。卷積性質的逆形式為 ,即兩個函式卷積的富里埃逆變換等於它們各自的富里埃逆變換的乘積乘以 。
帕塞瓦爾定理
 富里埃變換
富里埃變換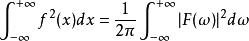 富里埃變換
富里埃變換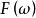 富里埃變換
富里埃變換 富里埃變換
富里埃變換若函式 可積且平方可積,則 。其中 是 的富里埃變換。
 富里埃變換
富里埃變換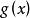 富里埃變換
富里埃變換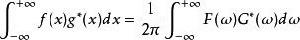 富里埃變換
富里埃變換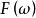 富里埃變換
富里埃變換 富里埃變換
富里埃變換 富里埃變換
富里埃變換 富里埃變換
富里埃變換 富里埃變換
富里埃變換更一般化而言,若函式 和 皆為平方可積函式,則 。其中 和 分別是 和 的富里埃變換, 代表復共軛。
