定義
全電流
一般情形下,通過空間某截面的電流應包括傳導電流與位移電流,其和稱全電流(total current) 。
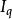 全電流定律
全電流定律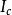 全電流定律
全電流定律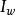 全電流定律
全電流定律假定為全電流, 為傳導電流或運動電流,為位移電流:
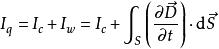 全電流定律
全電流定律 全電流定律
全電流定律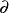 全電流定律
全電流定律(D為電通密度,S為截面面積, 表示偏微分符號,下同)
全電流是連續的,在空間構成閉合迴路。導線中有傳導電流(一般,導體中也有很小的位移電流),而電容器中有位移電流,即傳導電流中斷處,有位移電流接上。
定律
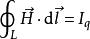 全電流定律
全電流定律麥克斯韋將安培環路定理推廣為全電流定律,可表示為: ,也即
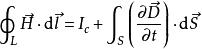 全電流定律
全電流定律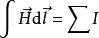 全電流定律
全電流定律當閉合回線可分為幾段,閉合回線的分段原則是:磁場強度相同,截面積相同,材料相同;而每段內H為常量,並和線段方向一致,沿閉合回線總磁壓為各段磁壓的代數和。這種情況下全電流定律又可表示為
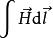 全電流定律
全電流定律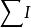 全電流定律
全電流定律其中, 是磁場強度矢量沿任意閉合線(常取磁通作為閉合回線)的線積分; 是穿過閉合回線所圍面積的電流代數和.
安培換路定律電流正負的規定:任意選定一個閉合回線的圍繞方向,凡是電流方向與閉合回線圍繞方向之間符合右螺鏇定則的電流作為正,反之為負;在均勻磁場中,HL=IN,H=IN/L。
推導
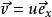 全電流定律
全電流定律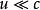 全電流定律
全電流定律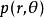 全電流定律
全電流定律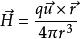 全電流定律
全電流定律設真空中有一電荷+q,在X 軸正方向以速度 運動( )。在t 時刻位置在A 處,如圖1所示, 則該時刻,電荷+q在空間一點 所產生的磁場H可由畢奧-薩伐爾定律求得:
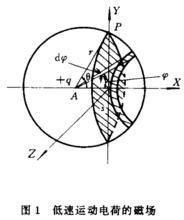 低速運動電荷的磁場
低速運動電荷的磁場其中r是粒子到觀察者的位置矢量。沿X軸方向看去,H的方向為順時針方向,且以r與X軸夾θ角,鏇轉一周得到半徑為R的閉合曲線C上各點的H大小相等。
磁場強度H沿C順時針方向一周的線積分為:
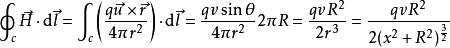 全電流定律
全電流定律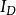 全電流定律
全電流定律設s是y-z平面上以c為邊界的圓面,則通過s面的位移電流 為:
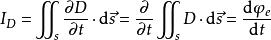 全電流定律
全電流定律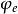 全電流定律
全電流定律這裡s不隨時間變化, 是穿過s面的電通量。
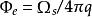 全電流定律
全電流定律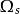 全電流定律
全電流定律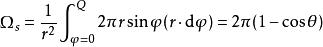 全電流定律
全電流定律由幾何關係可知,通過s面的電通量是 ,其中 是s在粒子處所張立體角。可以求得:當x <0 時,
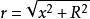 全電流定律
全電流定律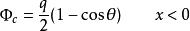 全電流定律
全電流定律其中, 是粒子到圓周c處的距離。因此:
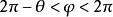 全電流定律
全電流定律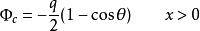 全電流定律
全電流定律當x>0時,積分遍及 , 則電通量是:
 與電荷位置對應的電通量
與電荷位置對應的電通量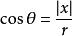 全電流定律
全電流定律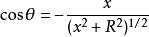 全電流定律
全電流定律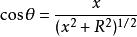 全電流定律
全電流定律 全電流定律
全電流定律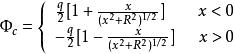 全電流定律
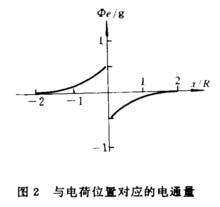
全電流定律以上兩式符合相反表明:當粒子在左邊時,電通量通過s面向右,而粒子在右邊時,電通量通過s面向左。因 ,x<0時, ;而當x > 0 時, ,因此 可以寫成:
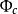 全電流定律
全電流定律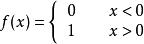 全電流定律
全電流定律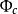 全電流定律
全電流定律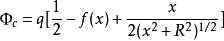 全電流定律
全電流定律注意到 在x=0處非連續,如圖2所示。因而可用單位階躍函式表示: ,因而 可以寫成:
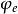 全電流定律
全電流定律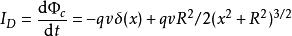 全電流定律
全電流定律根據階躍函式的性質,可求得 對時間的微商:
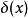 全電流定律
全電流定律其中 是狄拉克δ函式,此式對處在任意位置的粒子均成立。由此可求得磁場強度H沿C順時針方向一周的線積分為:
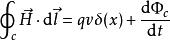 全電流定律
全電流定律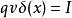 全電流定律
全電流定律上式中 是粒子穿過s面的瞬時電流,這一點可以用下述方法推證。
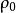 全電流定律
全電流定律 全電流定律
全電流定律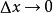 全電流定律
全電流定律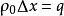 全電流定律
全電流定律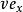 全電流定律
全電流定律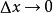 全電流定律
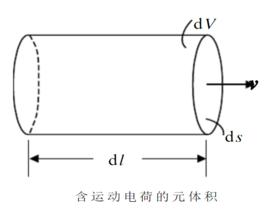
全電流定律考慮一線電荷密度為 ,長度為 的帶電棒,當 時, 保持不變,假定該棒以速度 沿x軸運動,當 時,該棒變成點電荷,其磁場強度由上式給出,當棒的中心處在原點的這一瞬間,沿x軸的線電荷密度是:
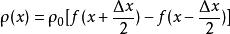 全電流定律
全電流定律因而通過Y-Z平面的粒子電流即運流電流是
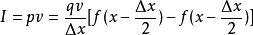 全電流定律
全電流定律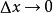 全電流定律
全電流定律上式求時的極限即得
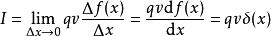 全電流定律
全電流定律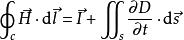 全電流定律
全電流定律因而磁場強度H沿C順時針方向一周的線積分可寫成:
這就是全電流定律的表達式。
討論
適用情況
全電流定律既適用於電流恆定情況,又適用於非恆定情況。
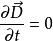 全電流定律
全電流定律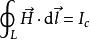 全電流定律
全電流定律對恆定情況, ,有
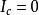 全電流定律
全電流定律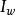 全電流定律
全電流定律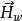 全電流定律
全電流定律若所討論的問題中, ,則磁場僅由位移電流( )產生(其磁場寫作 )
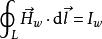 全電流定律
全電流定律即:
變化磁場電場
對比如下兩方程 :
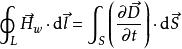 全電流定律
全電流定律變化的電場產生磁場:
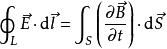 全電流定律
全電流定律變化的磁場產生感應電場: (B為磁通密度)
可見兩方程非常對稱。其不同點在於變化電場和產生的磁場之間為右手螺鏇關係,變化磁場和感生電場之間為左手螺鏇關係。
位移電流假說
1.麥克斯韋提出假說:變化的磁場在其周圍空間會激發一種渦鏇狀的非靜電場強,稱為渦鏇電場。並以此為基礎總結出了電場的環路定理。
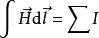 全電流定律
全電流定律2.對於穩恆電流,磁場滿足安培環路定理:
這個定理表明,磁場強度沿任意閉合迴路的線積分等於穿過以該閉合迴路為邊界曲面的傳導電流的代數和。但是,以閉合迴路為邊界的曲面原則上有無窮多個。也就是說,在穩恆電流情況下,對於以閉合迴路為邊界的所有曲面而言,安培環路定理總是成立的。但是,對於非穩恆電流,情況將不是這樣的。
比如取電容器兩極板間為一閉合的曲面,但是由於其中沒有傳導電流,所以安培環路定理右邊為零;但是不在兩極板間取的迴路,明顯電流和不是為零的,導致運用安培環路定理的時候出現了矛盾。
所以麥克斯韋大膽的提出假說:變化的電場能在其周圍激發磁場。
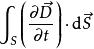 全電流定律
全電流定律並將 定義為位移電流,那么在上面講的例子當中,取在兩個極板之間的迴路,再套用安培環路定理就是成立的了,但是此時等式右邊的電流不是單獨的傳導電流,而是加上假說提出的位移電流。
正是如此,麥克斯韋進一步完善了他的電磁場理論,由此他毅然提出了全電流定理,以來完善安培環路定理的缺陷,就如上面的表述。
通過以上的研究,麥克斯韋完善了他的電磁場理論。