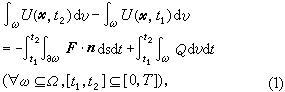守恆格式
正文
一類差分格式。如果差分格式的解滿足微分方程所描述的守恆律的離散模型,就稱它是該微分方程的守恆格式。描述d 維空間 Rd 中的一個區域Ω內、在時間間隔【0,T】上物理量U(尣,t)的守恆性質,一般可以用積分關係式表示為
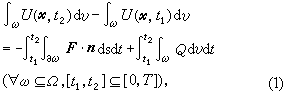
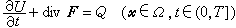 (2)
(2)
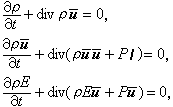
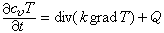 (3)
(3)
守恆格式一般是從積分守恆關係式(1)出發,利用積分插值方法建立起來的。首先將區域Ω剖分為一組子區域{ωj}。取(1)中的積分區域ω為任一ωj,t2=t1+Δt。然後將(1)中的積分用離散化的近似公式代替。如果 ωj與ωj是兩個相鄰的子區域,它們的邊界就有共同的部分Γij。當Γij 作為ωj的邊界和作為ωj的邊界時,其上的外法線方向n正好相反,所以當
 時,流量
時,流量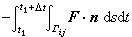 離散化以後的表達式應該只差一個負號。這意味著從一個子區域流出的物理量全部流入相鄰的子區域,因而保持了守恆的性質,這樣就得到守恆格式。
離散化以後的表達式應該只差一個負號。這意味著從一個子區域流出的物理量全部流入相鄰的子區域,因而保持了守恆的性質,這樣就得到守恆格式。 一維(d=1)守恆律的守恆格式的一般形式為
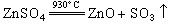 ,
,
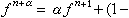
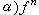 ,
,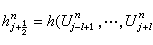 是和
是和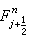 相容的。對於二維(d=2)問題的守恆格式,以拋物型方程
相容的。對於二維(d=2)問題的守恆格式,以拋物型方程 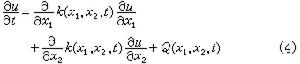
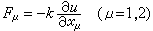 。
。
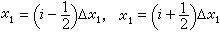
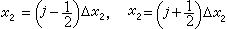
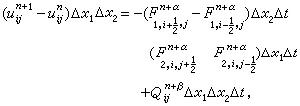
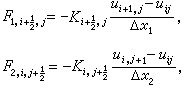
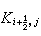 可取作
可取作 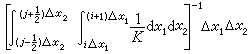
守恆格式的優點在於它的解能比較好地反映物理量基本的守恆性質。同時,由於守恆格式可以看作是從積分守恆關係式(1)出發建立的,對於間斷解,微分方程(2)是不成立的,但是積分關係式(1)仍然滿足,因此用守恆格式來計算間斷解往往不失為一種有效的方法。
參考書目
馮康等編:《數值計算方法》,國防工業出版社,北京,1978。