人物簡介
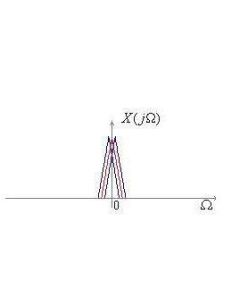
 奈奎斯特抽樣定律
奈奎斯特抽樣定律奈奎斯特,1889年出生在瑞典的尼爾斯比。1976年在德克薩斯逝世。奈奎斯特對資訊理論做出了重大的貢獻。奈奎斯特1907年移民到美國並於1912
年進入北達克塔大學學習。1917年在耶魯大學獲得物理學學位。1917年~1934年在 AT&T公司工作,後轉入實驗室工作。作為貝爾電話實驗室的,在(Johnson-Nyquist noise)和反饋放大器穩定性方面做出了很大的貢獻他早期的理論性工作是關於確定傳輸信息的需滿足的頻寬要求,在《貝爾系統技術》期刊上發表了《影響電報速度傳輸速度的因素》文章,為後來香農的資訊理論奠定了基礎。
1927年,奈奎斯特確定了如果對某一頻寬的有限時間連續信號()進行抽樣,且在抽樣率達到一定數值時,根據這些抽樣值可以在接收端準確地恢復原信號。為不使原波形產生“半波損失”,採樣率至少應為信號最高頻率的兩倍,這就是著名的奈奎斯特採樣定理。奈奎斯特1928年發表了《傳輸理論的一定論題》。
1954年,他從貝爾實驗室退休。
相關定律
(1)奈奎斯特採樣定理 :當採樣頻率fs.max大於信號中最高頻率fmax的2倍時,即:fs.max>=2fmax,則採樣之後的數位訊號完整地保留了原始信號中的信息;採樣定理是信息量化的基礎,使離散的2璡制比特表示連續的模擬量的理論依據。(2)奈氏準則(奈奎斯特第一準則):1924年,奈奎斯特(Nyquist)就推導出在理想低通信道下的最高碼元傳輸速率的公式:
 奈奎斯特抽樣定律
奈奎斯特抽樣定律驗證奈奎斯特第一準則
驗證奈奎斯特第一準則
理想低通信道下的最高碼元傳輸速率=2W Baud
其中W是理想低通信道的頻寬,單位為赫茲;Baud是波特,即碼元傳輸速率的單位,1波特為每秒傳送1個碼元。
奈氏準則的另一種表達方法是:每赫茲頻寬的理想低通信道的最高碼元傳輸速率是每秒2個碼元。若碼元的傳輸速率超過了奈氏準則所給出的數值,則將出現碼元之間的互相干擾,以致在接收端就無法正確判定碼元是1還是0。
對於具有理想帶通矩形特性的信道(頻寬為W),奈氏準則就變為:
理想帶通信道的最高碼元傳輸速率=1W Baud
即每赫寬頻的帶通信道的最高碼元傳輸速率為每秒1個碼元。
利用奈氏準則可以做一些簡單的估算例如: WCDMA的碼片速率為3.84Mps 如果採用16QAM調製方式最大可以得到的極限信息傳輸速率為3.84*4==15.36Mb/s,HSDPA技術採用16QAM調製方式的極限速度為14.4Mb/s。如果想得到更高的速率就要採用高階的調製方式。