多因素方差分析的概念
多因素方差分析用來研究兩個及兩個以上控制變數是否對觀測變數產生顯著影響。多因素方差分析不僅能夠分析多個控制變數對觀測變數的獨立影響，更能夠分析多個控制變數的互動作用能否對觀測變數產生顯著影響，最終找到利於觀測變數的最優組合 。
多因素方差分析的基本步驟
多因素方差分析實質也採用了統計推斷的方法，其基本步驟與假設檢驗完全一致 。
1．提出原假設
多因素方差分析的第一步是明確觀測變數和若干個控制變數，並在此基礎上提出原假設。
多因素方差分析的原假設是：各控制變數不同水平下觀測變數各總體的均值無顯著性差異，控制變數各效應和互動作用效應同時為0，即控制變數和它們的互動作用沒有對觀測變數產生顯著影響。
2．觀測變數方差的分解
在多因素方差分析中，觀測變數取值的變動會受到三個方面的影響：第一，控制變數獨立作用的影響，指單個控制變數獨立作用對觀測變數的影響；第二，控制變數互動作用的影響，指多個控制變數相互搭配後對觀測變數產生的影響；第三，隨機因素的影響，主要指抽樣誤差帶來的影響。基於上述原則，多因素方差分析將觀測變數的總變差分解為(以兩個控制變數為例)：
SST=SSA+SSB+SSAB+SSE (1)
其中，SST為觀測變數的總變差；SSA、SSB分別為控制變數A、B獨立作用引起的變差；SSAB為控制變數A、B兩兩互動作用引起的變差；SSE為隨機因素引起的變差。通常稱SSA+SSB+SSAB為主效應，SSAB為N向(N-WAY)互動效應，SSE為剩餘。其中，SST的定義為：
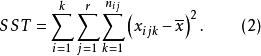多因素方差分析
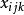多因素方差分析
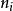多因素方差分析
多因素方差分析式(2)中，k為第i控制變數的水平數；r為第j控制變數的水平數；為控制變數A第i個水平和控制變數B第j個水平下第k樣本值；為控制變數A第i水平和控制變數B第j個水平下樣本個數；為觀測變數均值。
SSA的定義為：
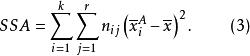多因素方差分析
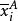多因素方差分析式(3)中，n為控制變數A第i個水平和控制變數B第j個水平下樣本觀測值個數，為控制變數A第i個水平下觀測變數的均值。
SSB的定義為：
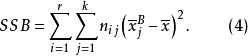多因素方差分析
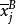多因素方差分析式(4)中，為控制變數B第j水平下觀測變數的均值。
SSE的定義為：
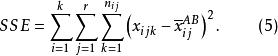多因素方差分析
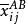多因素方差分析式(5)中，為控制變數A、B在i、j水平下觀測變數的均值。於是，互動作用可解釋的變差為：
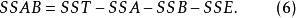多因素方差分析3．比較觀測變數總離差平方和各部分所占的比例，計算檢驗統計量的觀測值和相伴機率P值
多因素方差分析的第三步是通過比較觀測變數總離差平方和各部分所占的比例，推斷控制變數以及控制變數的互動作用是否給觀測變數帶來了顯著影響。容易理解，在觀測變數總離差平方和中，如果SSA所占比例較大，則說明控制變數A是引起觀測變數變動的主要因素之一，觀測變數的變動可以部分地由控制變數A來解釋；反之，如果SSA所占比例較小，則說明控制變數A不是引起觀測變數變動的主要因素，觀測變數的變動無法通過控制變數A來解釋。對SSB和SSAB同理。
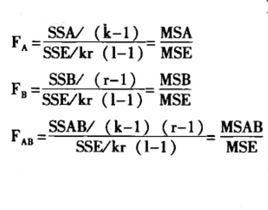
在多因素方差分析中，控制變數可以進一步劃分為固定效應和隨機效應兩種類型。其中，固定效應通常指控制變數的各個水平是可以嚴格控制的，它們給觀測變數帶來的影響是固定的；隨機效應是指控制變數的各個水平無法作嚴格的控制，它們給觀測變數帶來的影響是隨機的。一般來說，區分固定效應和隨機效應比較困難。由於這兩種效應的存在，多因素方差分析模型也有固定效應模型和隨機效應模型之分。這兩種模型分解觀測變數變差的方式是完全相同的，主要差別體現在檢驗統計量的構造方面。多因素方差分析採用的檢驗統計量仍為F統計量。如果有A、B兩個控制變數，通常對應三個F檢驗統計量。
在固定效應模型中，各F檢驗統計量為：
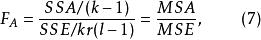多因素方差分析
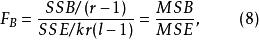多因素方差分析
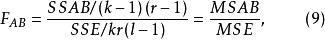多因素方差分析在隨機效應模型中，F統計量同式(9)，其他兩個F檢驗統計量為：
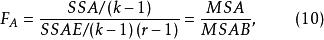多因素方差分析
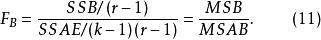多因素方差分析SPSS自動計算F統計量，並依據F分布表給出相伴機率P值。
多因素方差分析4．給定顯著性水平，並做出決策
多因素方差分析 多因素方差分析 多因素方差分析給出顯著性水平，與檢驗統計量的相伴機率P值作比較。在固定效應模式中，如果F的相伴機率P值小於或等於給定的顯著性水平，則應拒絕原假設，認為控制變數A不同水平下觀測變數各總體均值有顯著差異，控制變數A的各個效應不同時為0，控制變數A的不同水平對觀測變數產生了顯著影響；相反，如果F的相伴機率P值大於給定的顯著性水平，則不應拒絕原假設，認為控制變數A不同水平下觀測變數各總體均值無顯著差異，控制變數A的各個效應同時為0，控制變數A的不同水平對觀測變數沒有產生顯著影響。對控制變數B和A、B互動作用的推斷同理。在隨機模型中，應首先對A、B的互動作用是否顯著進行推斷，然後再分別依次對A、B的效應進行檢驗 。
