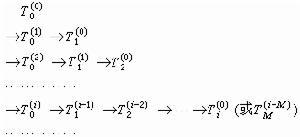外推極限法

外推極限法是通過對序列若干項的適當組合來推算序列極限的更精確近似值的方法，簡稱外推法。

外推極限法

例如,計算圓周率π，即直徑為1的圓的周長時,利用外推極限法，只要通過對上述圓的內接正二、三、四、六、八邊形等五個正多邊形的周長的計算（圓內接正二邊形的周長等於直徑的二倍）,即可得出π的接近9位有效數字的近似值T孈=3.141592648。計算過程如下面形式：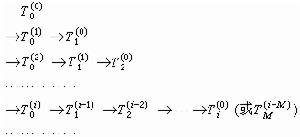

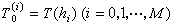其中,表示第i+1個正多邊形的周長，其邊數為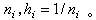而計算過程可用公式表達為

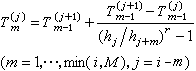(1)

式中M=4,r=2。算法(1)的推導利用了正n邊形周長T(h)

的展開式

一般情形下，設T(h)是一個問題的近似解，當h→0時，它的極限為τ0，T(h)具有展開式

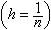
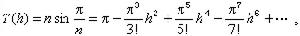
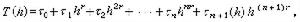
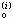式中τ1,τ2,…,τn為常數，τn+1(h)對h有界,那么都可套用算法（1）,通過已算出的值T=T(hi)(hi≠0,i=0,1,…)來推算τ0的更精確的近似值。
這種算法的思想,是通過T(hi),T(hi+1),…,T(hi+m)的線性組合,消去τ0的近似b值T(h)展開式中所含hr的低次誤差項，使得

這一方法的實質，是用滿足插值條件

　

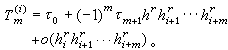
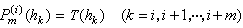
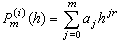　的多項式來代替T(h),用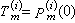來近似表示τ0的值，因此它又稱作多項式外推法。
如將插值多項式p嫑(h)改為其他插值函式，則得到其他的外推法，諸如有理式外推法、ε算法等。
外推極限法廣泛地套用於數值積分、微分方程和積分方程求解等方面。
參考書目
　鄧建中著：《外推法及其套用》，上海科學技術出版社，上海，1984。