簡介
早在文藝復興時期,偉大的藝術家、科學家和工程師達·芬奇對壓桿做了一些開拓性的研究工作。荷蘭物理學教授穆申布羅克(MusschenbroekPvan)於1729年通過對於木桿的受壓實驗,得出“壓曲載荷與桿長的平方成反比的重要結論”。
發展歷史
 壓桿穩定
壓桿穩定詳細介紹
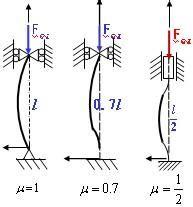
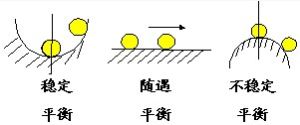
當細長桿件受壓時,卻表現出與強度失效全然不同的性質。例如一根細長的竹片受壓時,開始軸線為直線,接著必然是被壓彎,發生頗大的彎曲變形,最後折斷。與此類似,工程結構中也有很多受壓的細長桿。例如內燃機配氣機構中的挺桿,在它推動搖臂打開氣閥時,就受壓力作用。又如磨床液壓裝置的活塞桿當驅動工作檯向右移動時,油缸活塞上的壓力和工作檯的阻力使活塞桿受到壓縮。同樣,內燃機、空氣壓縮機、蒸汽機的連桿也是受壓桿件。還有,桁架結構中的抗壓桿、建築物中的柱也都是壓桿。現以圖四所示兩端鉸支的細長壓桿來說明這類問題。設壓力與桿件軸線重合,當壓力逐漸增加,但小於某一極限值時,桿件一直保持直線形狀的平衡,即使用微小的側向干擾力使其暫時發生輕微彎曲,干擾力解除後,它仍將恢復直線形狀。這表明壓桿直線形狀的平衡是穩定的。當壓力逐漸增加到某一極限值時,壓桿的直線平衡變為不穩定,將轉變為曲線形狀的平衡。這時如再用微小的側向干擾力使其發生輕微彎曲,干擾力解除後,它將保持曲線形狀的平衡,不能恢復原有的直線形狀。上述壓力的極限值稱為臨界壓力或臨界力,記為Fcr。壓桿喪失其直線形狀的平衡而過渡為曲線平衡,稱為喪失穩定,簡稱失穩,也稱為屈曲。
桿件失穩後,壓力的微小增加將引起彎曲變形的顯著增大,桿件已喪失了承載能力。這是因失穩造成的失效,可以導致整個機器或結構的損壞。但細長壓桿失穩時,應力並不一定很高,有時甚至低於比例極限。可見這種形式的失效,並非強度不足,而是穩定性不夠。
存在問題
除壓桿外,其他構件也存在穩定失效問題。例如在內壓作用下的圓柱形薄殼,壁內應力為拉應力,這就是一個強度問題。蒸汽鍋爐、圓柱形薄壁容器就是這種情況;但如圓柱形薄殼在均勻外壓作用下,壁內應力變為壓應力,則當外壓到達臨界值時,薄殼的圓形平衡就變為不穩定,會突然變成由虛線表示的長圓形。與此相似,板條或工字梁在最大抗彎剛度平面內彎曲時,會因載荷達到臨界值而發生側向彎曲。薄殼在軸向壓力或扭矩作用下,會出現局部折皺。這些都是穩定性問題。