培恩洛茲三角形

前提為兩條長度相等的線段，假如一條線段兩端加上向外的兩條斜線，另一條線段兩端加上向內的兩條斜線，則前者要顯得比後者長得多。 培恩洛茲三角形，將三條長方形以不同的視角使其錯位地交織在一起，在三條長方體“不合理”（透視）的銜接中，不可思議地創造了一種視覺“扭曲”感，一種強力的視覺穿透力躍然於紙。仔細觀察分析這幅圖，便可發現我們的視覺被轉換了三個角度。按常理應得出三個不同時空的三角圖形。然而，把同一時空轉移為不同時空並巧妙地整合成一個三角形，一個全然是不可能的三角形，卻改變了人們的視覺經驗，使“不可能”成了實實在在的可能的視覺圖形。 彭羅斯三角（Penrose triangle）是不可能的物體中的一種。最早是由瑞典藝術家Oscar Reutersvärd在1934年製作。英國數學家羅傑·彭羅斯及其父親也設計及推廣此圖案，並在1958年2月份的《英國心理學月刊》（British Journal of Psychology）中發表，稱之為“最純粹形式的不可能”。 彭羅斯三角看起來像是一個固體，由三個截面為正方形的長方體所構成，三個長方體組合成為一個三角形，但兩長方體之間的夾角似乎又是直角。上述的性質無法在任何一個正常三維空間的物體上實現。這種物件只能存在於一些特定的歐氏三維流形中[1]。

基本信息

• 中文名：培恩洛茲三角形
• 英文名：Payne Lodz triangle

• 別稱：不可能三角形
• 套用學科：數學
• 適用領域範圍：素描

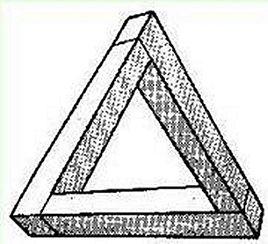
這種三角形又被稱為“不可思議三角形”，是悖理與比例逆反的典型體現。將三條長方形以不同的視覺角度使其錯位地交織在一起，在三條長方形“不合理”（透視）的銜接中，不可思議地創造了一種視覺“扭曲”感，一種強力的視覺穿透力躍然於紙上。

< 培恩洛茲三角形 >

它把同一時空轉移為不同時空並且巧妙地整合成一個三角形，一個全然悖理的三角形，卻改變了人們的視覺經驗，使“不可能”成了實實在在的可能的視覺圖形。

三角形每一個頂角都產生透視，儘管三個頂角各自體現不同角度的三角形。將三個頂角合成一個整體，就產生一個空間不可能圖形。

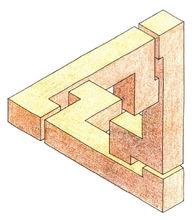培恩洛茲三角形

< 路透斯沃德的不可能的三角形 >